题目内容
如图，AC是⊙O的直径，∠ACB=60°，连接AB，过A、B两点分别作⊙O的切线，两切线交于点P．若已知⊙O的半径为1，则△PAB的周长为（ ）A、3
| ||
B、2
| ||
C、3
| ||
D、2
|
分析：由AC是⊙O的直径得∠ABC=90°，由∠BAC=30°，AC=2OC=2，得CB=1，AB=
；由AP为切线得∠CAP=90°，再由切线长定理知得△PAB为正三角形，从而求得△ABP的周长．
| 3 |
解答：解：∵AC是⊙O的直径，
∴∠ABC=90°，∠BAC=30°，CB=1，AB=
，
∵AP为切线，
∴∠CAP=90°，∠PAB=60°，
又∵AP=BP，
∴△PAB为正三角形，
∴周长=3
．
故选A．
∴∠ABC=90°，∠BAC=30°，CB=1，AB=
| 3 |
∵AP为切线，
∴∠CAP=90°，∠PAB=60°，
又∵AP=BP，
∴△PAB为正三角形，
∴周长=3
| 3 |
故选A．
点评：本题考查了圆的切线性质、切线长定理、直角三角形的性质等知识．属于基础题．
练习册系列答案
相关题目
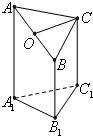如图是一个直三棱柱（以A1B1C1为底面）被一平面所截得到的几何体，截面为ABC．已知A1B1=B1C1=1，∠A1B1C1=90°，AA1=4，BB1=2，CC1=3．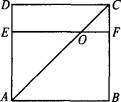
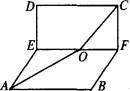
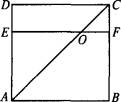
与直线
的夹角大小为
B．（不等式选讲）要使关于x的不等式
在实数