Question

已知{ a_n}是等差数列，{ b_n}是等比数列，S_n是{ a_n}的前n项和，a₁=b₁=1，S₂=．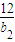
（Ⅰ）若b₂是a₁，a₃的等差中项，求a_n与b_n的通项公式；
（Ⅱ）若a_n∈N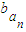^*，{}是公比为9的等比数列，求证：++…+＜．

Answer 1

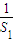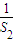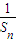【答案】分析：（I）设出等差数列的公差及等比数列的公比，将已知条件用就不量表示，求出公差与公比，利用等差及等比数列的通项公式求出两个数列的通项．
（II）将已知条件用公差与公比表示，解方程求出公差及公比，求出前n项和，利用放缩法证得不等式成立．
解答：解：设等差数列{a_n}的公差为d，等比数列{b_n}公比为q．
（Ⅰ）∵S₂=，∴a₁+a₁+d=，而a₁=b₁=1，则q（2+d）=12．①
又∵b₂是a₁，a₃的等差中项，
∴a₁+a₃=2b₂，得1+1+2d=2q，即1+d=q．②
联立①，②，解得或（4分）
所以a_n=1+（n-1）•2=2n-1，b_n=3^n-1；
或a_n=1+（n-1）•（-5）=6-5n，b_n=（-4）^n-1．（6分）
（Ⅱ）证明：∵a_n∈N^*，=b₁=q^{1+（n-1）d-1}=q^（n-1）d，
∴==q^d=9，即q^d=3²．①（8分）
由（Ⅰ）知q（2+d）=12，得q=．②
∵a₁=1，a_n∈N^*，∴d为正整数，从而根据①②知q＞1且q也为正整数，
∴d可为1或2或4，但同时满足①②两个等式的只有d=2，q=3，
∴a_n=2n-1，S_n==n²．（10分）
∴=＜=（-）（n≥2）．
当n≥2时，+++＜1+（-）+（-）+（-）++（-
=1+[（-）+（-）+（-）+（-）]
=1+（1+--）
=--＜．
显然，当n=1时，不等式成立．故n∈N^*，+++＜．（14分）
点评：证明一个数列的和满足的不等式时，先考虑是否能求出和再证；若和不能求，一般用放缩法证明．