题目内容
用数学归纳法证明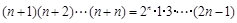 ,从
,从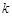 到
到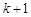 ,左边需要增乘的代数式为()
,左边需要增乘的代数式为()
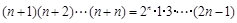 ,从
,从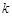 到
到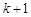 ,左边需要增乘的代数式为()
,左边需要增乘的代数式为()A. | B. | C. | D. |
B
试题分析:当n=k时,左边等于(k+1)(k+2)…(k+k)=(k+1)(k+2)…(2k),当n=k+1时,左边等于(k+2)(k+3)…(k+k)(2k+1)(2k+2),故从“k”到“k+1”的证明,左边需增添的代数式是
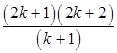 =2(2k+1),故答案为B.
=2(2k+1),故答案为B.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
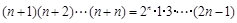 ,从
,从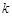 到
到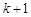 ,左边需要增乘的代数式为()
,左边需要增乘的代数式为()A. | B. | C. | D. |
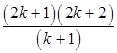 =2(2k+1),故答案为B.
=2(2k+1),故答案为B.
 阅读快车系列答案
阅读快车系列答案