题目内容
定义:如果函数y=f(x)(x∈D)满足(1)f(x)在D上是单调函数;(2)存在闭区间|a,b|⊆D,使f(x)在区间[a,b]上值域也是[a,b],则称f(x)为闭函数,则下列函数:
(1)f(x)=x2+2x,x∈[-1,+∞);(2)f(x)=x3,x∈[-2,3];(3)f(x)=lgx,x∈[1,+∝)
其中是闭函数的是
(1)f(x)=x2+2x,x∈[-1,+∞);(2)f(x)=x3,x∈[-2,3];(3)f(x)=lgx,x∈[1,+∝)
其中是闭函数的是
(1)(2)
(1)(2)
.(只填序号)分析:利用闭函数的定义,对于(1)(2)(3)单调性显然,关键是找出闭区间,使得结论成立.
解答:解:(1)f(x)=(x+1)2-1,对称轴为x=-1,存在闭区间[-1,1],显然满足,故是闭函数;(2)f(x)=x3,在x∈[-2,3]上是单调增函数.存在闭区间[-1,1],故是闭函数;(3)f(x)=lgx,x∈[1,+∝)是单调增函数,由于x=lgx有且只有一解,故不满足存在闭区间|a,b|⊆D,使f(x)在区间[a,b]上值域也是[a,b]
故答案是:(1)(2)
故答案是:(1)(2)
点评:这是个知识迁移题,这类问题一般是考查学生的类比猜想能力、探索问题的能力.这类问题是近年高考命题的一个亮点,很能考查学生的分析问题、探索问题的潜在的能力.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
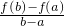 ,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.如y=x4是[-1,1]上的平均值函数,0就是它的均值点.
,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.如y=x4是[-1,1]上的平均值函数,0就是它的均值点.