题目内容
函数f(x)=loga(3-ax)(a>0,a≠1)
(1)当a=2时,求函数f(x)的定义域;
(2)是否存在实数a,使函数f(x)在[1,2]递减,并且最大值为1,若存在,求出a的值;若不存在,请说明理由.
解:(1)当a=2时,f(x)=log2(3-2x)
∴3-2x>0
解得
即函数f(x)的定义域(-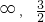 )
)
(2)假设存在满足条件的a,
∵a>0且a≠1,令t=3-ax,则t=3-ax为单调递减的函数
由复合函数的单调性可知,y=logat在定义域上单调递增,且t=3-ax>0在[1,2]上恒成立
∴a>1且由题可得f(1)=1,3-2a>0,
∴loga(3-a)=1,2a<3
∴3-a=a,且a
故a的值不存在
分析:(1)由题意可得,3-2x>0,解不等式可求函数f(x)的定义域
(2)假设存在满足条件的a,由a>0且a≠1可知函数t=3-ax为单调递减的函数,则由复合函数的单调性可知,y=logat在定义域上单调递增,且t=3-ax>0在[1,2]上恒成立,f(1)=1,从而可求a的范围
点评:本题主要考查了对数函数定义域的求解,对数函数与一次函数复合而成的复合函数的单调性的应用,解题中要注意,不要漏掉真数t=3-ax>0的要求
∴3-2x>0
解得

即函数f(x)的定义域(-
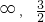 )
)(2)假设存在满足条件的a,
∵a>0且a≠1,令t=3-ax,则t=3-ax为单调递减的函数
由复合函数的单调性可知,y=logat在定义域上单调递增,且t=3-ax>0在[1,2]上恒成立
∴a>1且由题可得f(1)=1,3-2a>0,
∴loga(3-a)=1,2a<3
∴3-a=a,且a

故a的值不存在
分析:(1)由题意可得,3-2x>0,解不等式可求函数f(x)的定义域
(2)假设存在满足条件的a,由a>0且a≠1可知函数t=3-ax为单调递减的函数,则由复合函数的单调性可知,y=logat在定义域上单调递增,且t=3-ax>0在[1,2]上恒成立,f(1)=1,从而可求a的范围
点评:本题主要考查了对数函数定义域的求解,对数函数与一次函数复合而成的复合函数的单调性的应用,解题中要注意,不要漏掉真数t=3-ax>0的要求

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知函数f(x)=log -
(x2-ax+3a)在[2,+∞)上是减函数,则实数a的范围是( )
| 1 |
| 2 |
| A、(-∞,4] |
| B、(-4,4] |
| C、(0,12) |
| D、(0,4] |