题目内容
(2013•青岛二模)已知函数f(x)=
x3-ax2+(a2-1)x+ln(a+1)(其中a为常数)
(Ⅰ)若f(x)在区间(-1,1)上不单调,求a的取值范围;
(Ⅱ)若存在一条与y轴垂直的直线和函数Γ(x)=f(x)-(a2-1)x+lnx的图象相切,且切点的横坐标x0满足x0>2,求实数a的取值范围;
(Ⅲ)记函数y=f(x)的极大值点为m,极小值点为n,若2m+5n≥
对于x∈[0,π]恒成立,试求a的取值范围.
| 1 |
| 3 |
(Ⅰ)若f(x)在区间(-1,1)上不单调,求a的取值范围;
(Ⅱ)若存在一条与y轴垂直的直线和函数Γ(x)=f(x)-(a2-1)x+lnx的图象相切,且切点的横坐标x0满足x0>2,求实数a的取值范围;
(Ⅲ)记函数y=f(x)的极大值点为m,极小值点为n,若2m+5n≥
| ||
| cosx+2 |
分析:(Ⅰ)先对函数求导,由函数f(x)在区间(-1,1)不单调,可知f‘(x)在(-1,1)上存在零点,结合函数的零点定理可求a的范围
(Ⅱ)先对已知函数求导可得,Γ′(x)=x2-2ax+
,由题意设切点的横坐标x0,从而可得x02-2ax0+
=0,分离可得a=
(x0+
),结合函数y=x+
的单调性可求函数的取值范围,进而可求a的范围
(Ⅲ)多函数求导可得f'(x)=x2-2ax+a2-1,然后研究函数的单调性,进而可确定极大值及极小值,由2m+5n≥
对于x∈[0,π]恒成立可建立关于a的不等式,可求
(Ⅱ)先对已知函数求导可得,Γ′(x)=x2-2ax+
| 1 |
| x |
| 1 |
| x0 |
| 1 |
| 2 |
| 1 |
| x02 |
| 1 |
| x2 |
(Ⅲ)多函数求导可得f'(x)=x2-2ax+a2-1,然后研究函数的单调性,进而可确定极大值及极小值,由2m+5n≥
| ||
| cosx+2 |
解答:(本小题满分13分)
解:(Ⅰ)∵f(x)=
x3-ax2+(a2-1)x+ln(a+1),
∴f'(x)=x2-2ax+a2-1
因为函数f(x)在区间(-1,1)不单调,所以函数f'(x)在(-1,1)上存在零点.
而f'(x)=0的两根为a-1,a+1,区间长为2,
∴f'(x)在区间(-1,1)上不可能有2个零点.
所以f'(-1)f'(1)<0,…(2分)
即a2(a+2)(a-2)<0,又由题意可知:a>-1
∴a∈(-1,0)∪(0,2).…(3分)
(Ⅱ)Γ(x)=f(x)-(a2-1)x+lnx=
x3-ax2+lnx+ln(a+1),Γ′(x)=x2-2ax+
,
∵存在一条与y轴垂直的直线和函数Γ(x)=f(x)-(a2-1)x+lnx的图象相切,且切点的横坐标x0,
∴Γ′(x0)=x02-2ax0+
=0⇒a=
(x0+
),(x0>2)…(5分)
令h(x)=
(x+
)(x>2),则h′(x)=
(1-
)
当x>2时,h′(x)=
(1-
)>0,
∴h(x)=
(x+
)在(2,+∞)上为增函数,
从而h(x0)=
(x0+
)>h(2)=
,又由题意可知:a>-1
∴a>
…(8分)
(Ⅲ)f'(x)=x2-2ax+a2-1,
由f'(x)=0得:x=a-1,或x=a+1,
当x变化时,f(x),f'(x)变化如下表
由表可知:f(x)的极大值点m=a-1,极小值点n=a+1
∴2m+5n=7a+3…(10分)
令h(x)=
,x∈[0,π],则h′(x)=
,
由h′(x)=0⇒x=
,
当x∈[0,
)时,h'(x)>0,当x∈(
,π]时,h'(x)<0,
∴当x=
时,h(x)取最大值为h(
)=1,…(12分)
为满足题意,必须2m+5n≥h(x)max,所以7a+3≥1,
又由题意可知:a>-1,
∴a≥-
…(13分)
解:(Ⅰ)∵f(x)=
| 1 |
| 3 |
∴f'(x)=x2-2ax+a2-1
因为函数f(x)在区间(-1,1)不单调,所以函数f'(x)在(-1,1)上存在零点.
而f'(x)=0的两根为a-1,a+1,区间长为2,
∴f'(x)在区间(-1,1)上不可能有2个零点.
所以f'(-1)f'(1)<0,…(2分)
即a2(a+2)(a-2)<0,又由题意可知:a>-1
∴a∈(-1,0)∪(0,2).…(3分)
(Ⅱ)Γ(x)=f(x)-(a2-1)x+lnx=
| 1 |
| 3 |
| 1 |
| x |
∵存在一条与y轴垂直的直线和函数Γ(x)=f(x)-(a2-1)x+lnx的图象相切,且切点的横坐标x0,
∴Γ′(x0)=x02-2ax0+
| 1 |
| x0 |
| 1 |
| 2 |
| 1 |
| x02 |
令h(x)=
| 1 |
| 2 |
| 1 |
| x2 |
| 1 |
| 2 |
| 2 |
| x3 |
当x>2时,h′(x)=
| 1 |
| 2 |
| 2 |
| x3 |
∴h(x)=
| 1 |
| 2 |
| 1 |
| x2 |
从而h(x0)=
| 1 |
| 2 |
| 1 |
| x02 |
| 9 |
| 8 |
∴a>
| 9 |
| 8 |
(Ⅲ)f'(x)=x2-2ax+a2-1,
由f'(x)=0得:x=a-1,或x=a+1,
当x变化时,f(x),f'(x)变化如下表
| x | (-∞,a-1) | a-1 | (a-1,a+1) | a+1 | (a+1,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | 极大值 | 极小值 |
∴2m+5n=7a+3…(10分)
令h(x)=
| ||
| cosx+2 |
| ||
| (cosx+2)2 |
由h′(x)=0⇒x=
| 2π |
| 3 |
当x∈[0,
| 2π |
| 3 |
| 2π |
| 3 |
∴当x=
| 2π |
| 3 |
| 2π |
| 3 |
为满足题意,必须2m+5n≥h(x)max,所以7a+3≥1,
又由题意可知:a>-1,
∴a≥-
| 2 |
| 7 |
点评:本题主要考查了函数的导数在求解函数的单调性、函数的极值中的应用,函数的恒成立与函数的最值的相互转化关系的应用,属于函数知识的综合应用

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 (2013•青岛二模)一同学为研究函数f(x)=
(2013•青岛二模)一同学为研究函数f(x)=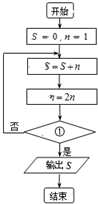 (2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )
(2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )