题目内容
有如下几个说法:①如果x1,x2是方程ax2+bx+c=0的两个实根且x1<x2,那么不等式ax2+bx+c<0的解集为{x|x1<x<x2};
②当△=b2-4ac<0时,二次不等式 ax2+bx+c>0的解集为∅;
③
 与不等式(x-a)(x-b)≤0的解集相同;
与不等式(x-a)(x-b)≤0的解集相同;④
 与x2-2x<3(x-1)的解集相同.
与x2-2x<3(x-1)的解集相同.其中正确说法的个数是( )
A.3
B.2
C.1
D.0
【答案】分析:通过给变量取特殊值,举反例可得这四个命题都不正确,由此得出结论.
解答:解:当二次项的系数a<0时,不等式ax2+bx+c<0的解集为{x|x1>x 或x>x2},①不正确.
当二次项的系数a>0时,若△=b2-4ac<0时,二次不等式ax2+bx+c>0的解集为R,故②不正确.
x=b在不等式(x-a)(x-b)≤0的解集中,但不在 的解集中,故③不正确.
的解集中,故③不正确.
当x-<0时, 即 x2-2x>3(x-1),故④不正确.
即 x2-2x>3(x-1),故④不正确.
故选D.
点评:本题主要考查一元二次方程的根与系数的关系,式不等式的解法,体现了化归与转化的数学思想.通过给变量取特殊值,举反例来说明某个命题不正确,是一种简单有效的方法,属于中档题.
解答:解:当二次项的系数a<0时,不等式ax2+bx+c<0的解集为{x|x1>x 或x>x2},①不正确.
当二次项的系数a>0时,若△=b2-4ac<0时,二次不等式ax2+bx+c>0的解集为R,故②不正确.
x=b在不等式(x-a)(x-b)≤0的解集中,但不在
 的解集中,故③不正确.
的解集中,故③不正确.当x-<0时,
 即 x2-2x>3(x-1),故④不正确.
即 x2-2x>3(x-1),故④不正确.故选D.
点评:本题主要考查一元二次方程的根与系数的关系,式不等式的解法,体现了化归与转化的数学思想.通过给变量取特殊值,举反例来说明某个命题不正确,是一种简单有效的方法,属于中档题.

练习册系列答案
相关题目

 是方程
是方程 的两个实根且
的两个实根且 ,那么不等式
,那么不等式 的解集为
的解集为 ;
; 时,二次不等式
时,二次不等式 的解集为
的解集为 ;
; 与不等式
与不等式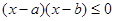 的解集相同;
的解集相同; 与
与 的解集相同.
的解集相同.