题目内容
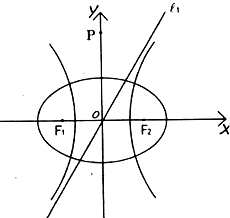 已知椭圆M:
已知椭圆M:| x2 |
| 8 |
| y2 |
| 4 |
| 3 |
(1)求双曲线N的方程;
(2)设直线l2过点P(0,4),且与双曲线N相交于A,B两点,与x轴交于点Q(Q与双曲线N的顶点不重合),若
| PQ |
| QA |
| QB |
| 8 |
| 3 |
分析:(1)由题意,设双曲线N的方程为:x2 -
=λ(λ>0),根据椭圆与双曲线的焦点相同,可求双曲线N的方程;
(2)由题意可知直线l2的斜率存在且不可能为0,设直线l2:x=m(y-4),与双曲线方程联立
,消去x可得:(3m2-1)y2-24m2y+48m2-3=0,进而可得y1+y2=
②,y1y2=
③,根据
=λ1
=λ2
,可得(4m,-4)=λ1(x1-4m,y1)=λ2(x2-4m,y2),利用λ1+λ2=-
,即可求得直线l2的方程.
| y2 |
| 3 |
(2)由题意可知直线l2的斜率存在且不可能为0,设直线l2:x=m(y-4),与双曲线方程联立
|
| 24m2 |
| 3m2-1 |
| 48m2-3 |
| 3m2-1 |
| PQ |
| QA |
| QB |
| 8 |
| 3 |
解答:解:(1)由题意,设双曲线N的方程为:x2 -
=λ(λ>0)
∵椭圆M:
+
=1的焦点为(-2,0),(2,0)
∴双曲线N:x2 -
=λ(λ>0)的焦点为(-2,0),(2,0)
∴λ+3λ=4
∴λ=1
∴双曲线N的方程为:x2 -
=1
(2)由题意可知直线l2的斜率存在且不可能为0,设直线l2:x=m(y-4),A(x1,y1),B(x2,y2)
∴Q(4m,0)
联立方程
,消去x可得:(3m2-1)y2-24m2y+48m2-3=0
∴3m2-1≠0,△=576m4-4(3m2-1)(48m2-3)>0①
y1+y2=
②,y1y2=
③
∵
=λ1
=λ2
,
∴(4m,-4)=λ1(x1-4m,y1)=λ2(x2-4m,y2)
∴-4=λ1y1=λ2y2
∴λ1=
,λ2=
∴λ1+λ2=
+
=-
④
由②③④可得:m2=
且满足①式
∴直线l2的方程为2x-y+4=0或2x+y-4=0
| y2 |
| 3 |
∵椭圆M:
| x2 |
| 8 |
| y2 |
| 4 |
∴双曲线N:x2 -
| y2 |
| 3 |
∴λ+3λ=4
∴λ=1
∴双曲线N的方程为:x2 -
| y2 |
| 3 |
(2)由题意可知直线l2的斜率存在且不可能为0,设直线l2:x=m(y-4),A(x1,y1),B(x2,y2)
∴Q(4m,0)
联立方程
|
∴3m2-1≠0,△=576m4-4(3m2-1)(48m2-3)>0①
y1+y2=
| 24m2 |
| 3m2-1 |
| 48m2-3 |
| 3m2-1 |
∵
| PQ |
| QA |
| QB |
∴(4m,-4)=λ1(x1-4m,y1)=λ2(x2-4m,y2)
∴-4=λ1y1=λ2y2
∴λ1=
| -4 |
| y1 |
| -4 |
| y2 |
∴λ1+λ2=
| -4 |
| y1 |
| -4 |
| y2 |
| 8 |
| 3 |
由②③④可得:m2=
| 1 |
| 4 |
∴直线l2的方程为2x-y+4=0或2x+y-4=0
点评:本题以椭圆方程为载体,考查双曲线的标准方程,考查直线与双曲线的位置关系,考查向量知识的运用,解题的关键是联立方程,进而利用向量知识进行转化.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
已知椭圆
+
=1与双曲线
-
=1有相同的焦点,则动点P(m,n)的轨迹为( )
| x2 |
| 16 |
| y2 |
| n2 |
| x2 |
| 8 |
| y2 |
| m |
| A、椭圆的一部分 |
| B、双曲线的部分 |
| C、抛物线的一部分 |
| D、直线的部分 |
已知椭圆
+
=1与双曲线
-
=1有相同的准线,则动点P(n,m)的轨迹为( )
| x2 |
| 4 |
| y2 |
| n |
| x2 |
| 8 |
| y2 |
| m |
| A、椭圆的一部分 |
| B、双曲线的一部分 |
| C、抛物线的一部分 |
| D、直线的一部分 |