题目内容
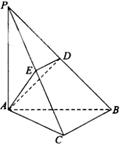
(本小题共13分) 如图,在三棱锥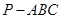 中,
中,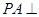 底面ABC
底面ABC
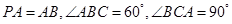 ,点
,点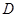 、
、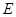 分别在棱
分别在棱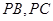 上,且
上,且
(Ⅰ)求证: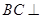 平面
平面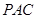 ;
;
(Ⅱ)当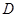 为
为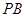 的中点时,求
的中点时,求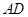 与平面
与平面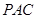 所成角的大小的余弦值;
所成角的大小的余弦值;
(Ⅲ)是否存在点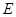 ,使得二面角
,使得二面角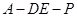 为直二面角?并说明理由.
为直二面角?并说明理由.
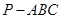 中,
中,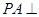 底面ABC
底面ABC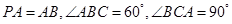 ,点
,点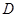 、
、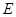 分别在棱
分别在棱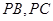 上,且
上,且
(Ⅰ)求证:
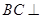 平面
平面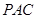 ;
;(Ⅱ)当
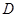 为
为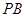 的中点时,求
的中点时,求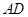 与平面
与平面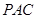 所成角的大小的余弦值;
所成角的大小的余弦值;(Ⅲ)是否存在点
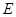 ,使得二面角
,使得二面角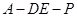 为直二面角?并说明理由.
为直二面角?并说明理由.
解:(Ⅰ)∵PA⊥底面ABC,∴PA⊥BC. 又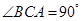 ,∴AC⊥BC.
,∴AC⊥BC.
又 ∴BC⊥平面PAC.————3分
∴BC⊥平面PAC.————3分
(Ⅱ)∵D为PB的中点,DE//BC, ∴ ,
,
又由(Ⅰ)知,BC⊥平面PAC, ∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,————5分
∵PA⊥底面ABC,∴PA⊥AB,又PA=AB,
∴△ABP为等腰直角三角形,∴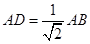 ,
,
∴在Rt△ABC中,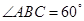 ,∴
,∴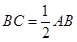 .
.
∴在Rt△ADE中, ,
,
∴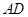 与平面
与平面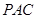 所成的角的大小的余弦值
所成的角的大小的余弦值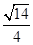 .————8分
.————8分
(Ⅲ)∵AE//BC,又由(Ⅰ)知,BC⊥平面PAC,∴DE⊥平面PAC,
又∵AE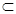 平面PAC,PE
平面PAC,PE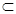 平面PAC,∴DE⊥AE,DE⊥PE,
平面PAC,∴DE⊥AE,DE⊥PE,
∴∠AEP为二面角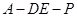 的平面角,
的平面角,
∵PA⊥底面ABC,∴PA⊥AC,∴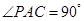 .
.
∴在棱PC上存在一点E,使得AE⊥PC,这时 ,
,
故存在点E使得二面角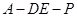 是直二面角.————13分
是直二面角.————13分
【解法2】如图,以A为原煤点建立空间直角坐标系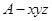 , ————1分
, ————1分
设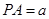 ,由已知可得
,由已知可得 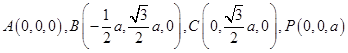 .
.
(Ⅰ)∵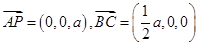 ,∴
,∴ ,∴BC⊥AP.
,∴BC⊥AP.
又∵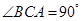 ,∴BC⊥AC,∴BC⊥平面PAC. ————3分
,∴BC⊥AC,∴BC⊥平面PAC. ————3分
(Ⅱ)∵D为PB的中点,DE//BC,∴E为PC的中点,
∴ , ∴又由(Ⅰ)知,BC⊥平面PAC,
, ∴又由(Ⅰ)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E. ∴∠DAE是AD与平面PAC所成的角,
∵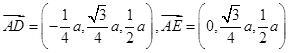 ,
,
∴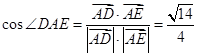 .————7分
.————7分
∴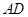 与平面
与平面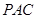 所成的角的大小的余弦值
所成的角的大小的余弦值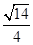 .————8分
.————8分
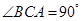 ,∴AC⊥BC.
,∴AC⊥BC.又
 ∴BC⊥平面PAC.————3分
∴BC⊥平面PAC.————3分(Ⅱ)∵D为PB的中点,DE//BC, ∴
 ,
,又由(Ⅰ)知,BC⊥平面PAC, ∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,————5分
∵PA⊥底面ABC,∴PA⊥AB,又PA=AB,
∴△ABP为等腰直角三角形,∴
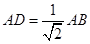 ,
,∴在Rt△ABC中,
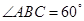 ,∴
,∴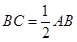 .
.∴在Rt△ADE中,
 ,
,∴
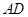 与平面
与平面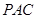 所成的角的大小的余弦值
所成的角的大小的余弦值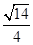 .————8分
.————8分(Ⅲ)∵AE//BC,又由(Ⅰ)知,BC⊥平面PAC,∴DE⊥平面PAC,
又∵AE
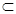 平面PAC,PE
平面PAC,PE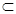 平面PAC,∴DE⊥AE,DE⊥PE,
平面PAC,∴DE⊥AE,DE⊥PE,∴∠AEP为二面角
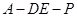 的平面角,
的平面角,∵PA⊥底面ABC,∴PA⊥AC,∴
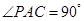 .
.∴在棱PC上存在一点E,使得AE⊥PC,这时
 ,
,故存在点E使得二面角
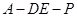 是直二面角.————13分
是直二面角.————13分【解法2】如图,以A为原煤点建立空间直角坐标系
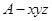 , ————1分
, ————1分设
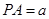 ,由已知可得
,由已知可得 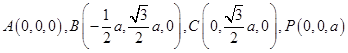 .
.(Ⅰ)∵
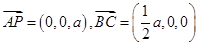 ,∴
,∴ ,∴BC⊥AP.
,∴BC⊥AP.又∵
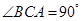 ,∴BC⊥AC,∴BC⊥平面PAC. ————3分
,∴BC⊥AC,∴BC⊥平面PAC. ————3分 (Ⅱ)∵D为PB的中点,DE//BC,∴E为PC的中点,
∴
 , ∴又由(Ⅰ)知,BC⊥平面PAC,
, ∴又由(Ⅰ)知,BC⊥平面PAC,∴DE⊥平面PAC,垂足为点E. ∴∠DAE是AD与平面PAC所成的角,
∵
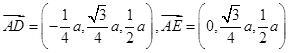 ,
,∴
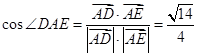 .————7分
.————7分∴
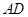 与平面
与平面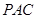 所成的角的大小的余弦值
所成的角的大小的余弦值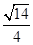 .————8分
.————8分略

练习册系列答案
相关题目
 的各棱长都是4,
的各棱长都是4,  是
是 的中点,动点
的中点,动点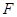 在侧棱
在侧棱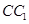 上,且不与点
上,且不与点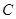 重合.
重合.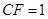 时,求证:
时,求证: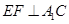 ;
;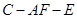 的大小为
的大小为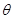 ,求
,求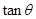 的最小值.
的最小值.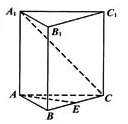
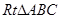 中,
中,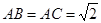 ,
,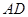 斜边
斜边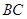 上的高,以
上的高,以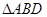 折 起,使
折 起,使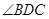 为直角。
为直角。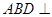 平面
平面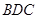 ;(2)求证:
;(2)求证: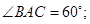
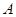 到平面
到平面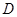 到平面
到平面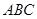 的距离;
的距离; 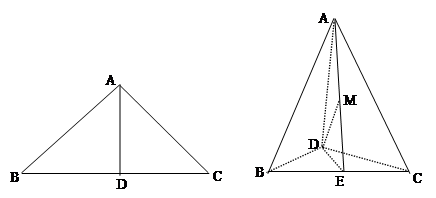
 ∥平面
∥平面 ,直线
,直线 ∥
∥ 平面
平面 ,
, ∩
∩ =
= 是圆柱的母线,
是圆柱的母线, 是圆柱底面圆的直径,
是圆柱底面圆的直径, 是底面圆周上异于
是底面圆周上异于 的任意一点,
的任意一点,
 平面
平面 ;
; 的体积的最大值.
的体积的最大值.
 ,底面边长为
,底面边长为 ,E是SA的中点,则异面直线BE与SC所成角的大小为 ( )
,E是SA的中点,则异面直线BE与SC所成角的大小为 ( )
 ⊥平面
⊥平面 ,
, ∥
∥ ,且
,且 是
是 的中点.
的中点.
 ∥平面
∥平面 ;
; ;
; 多面体的体积.
多面体的体积.
 ,
, ⊥
⊥ ,
, ⊥
⊥ ⊥
⊥ ;
; 所成的角相等;
所成的角相等; 在
在 .
.
 已知直线
已知直线 ,给出下列命题:
,给出下列命题: 且
且 ,则
,则
 ; ②若
; ②若 ;
; ; ④若
; ④若
