题目内容
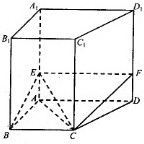（2010•南京三模）如图，直四棱柱ABCD-A1B1C1D1中，四边形ABCD是梯形，AD∥BC，AC⊥CD，E是AA1上的一点．（1）求证：CD⊥平面ACE；
（2）若平面CBE交DD1于点F，求证：EF∥AD．
分析：（1）要证CD⊥ACE，只需证明CD垂直平面ACE内的两条相交直线AC与AA1即可．
（2）平面CBE交DD1于点F，证明EF∥AD，只需证明BC∥平面ADD1A1，EF∥BC，即可．
（2）平面CBE交DD1于点F，证明EF∥AD，只需证明BC∥平面ADD1A1，EF∥BC，即可．
解答：证明：（1）因为直四棱柱ABCD-A1B1C1D1，所以AA1⊥平面ABCD，因为CD?平面ABCD，
所以AA1⊥CD，因为AC⊥DC，
AC?平面AEC，A1A∩AC=A，
所以CD⊥平面ACE
（2）因为AD∥BC，AD?平面ADD1A1，BC不在平面ADD1A1，所以BC∥平面ADD1A1，因为BC?平面BCE，
平面BCE∩平面ADD1A1=EF，所以EF∥BC，
因为AD∥BC，所以EF∥AD．
所以AA1⊥CD，因为AC⊥DC，
AC?平面AEC，A1A∩AC=A，
所以CD⊥平面ACE
（2）因为AD∥BC，AD?平面ADD1A1，BC不在平面ADD1A1，所以BC∥平面ADD1A1，因为BC?平面BCE，
平面BCE∩平面ADD1A1=EF，所以EF∥BC，
因为AD∥BC，所以EF∥AD．
点评：本小题主要考查空间线面关系、直线与平面垂直，直线与直线平行等知识，考查化归与转化的数学思想方法，以及空间想象能力、推理论证能力．
练习册系列答案
相关题目
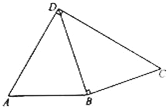（2010•南京三模）如图，平面四边形ABCD中，∠A=60°，AD⊥CD，DB⊥BC，AB=2