题目内容
(本小题满分12分)已知函数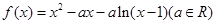 .
.
(1) 当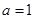 时,求函数
时,求函数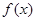 的最值;
的最值;
(2) 求函数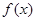 的单调区间;
的单调区间;
(3)(仅385班、389班学生做) 试说明是否存在实数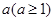 使
使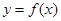 的图象与
的图象与 无公共点.
无公共点.
【答案】
解:(1) 函数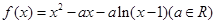 的定义域是
的定义域是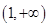 .
.
当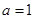 时,
时, ,所以
,所以 在
在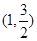 为减函数 ,
为减函数 ,
在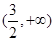 为增函数,所以函数f (x)的最小值为
为增函数,所以函数f (x)的最小值为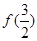 =
=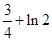 .
.
(2) 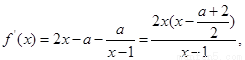
若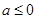 时,则
时,则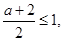 f(x)
f(x)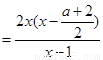
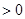 在
在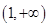 恒成立,
恒成立,
所以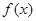 的增区间为
的增区间为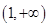 .
.
若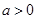 ,则
,则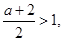 故当
故当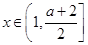 ,
,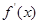
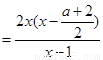
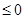 ,
,
当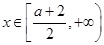 时,f(x)
时,f(x) 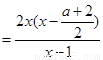
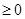 ,
,
所以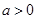 时
时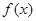 的减区间为
的减区间为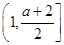 ,
,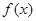 的增区间为
的增区间为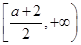 .
.
(3) 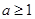 时,由(1)知
时,由(1)知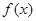 在
在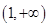 上的最小值为
上的最小值为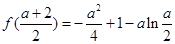 ,
,
令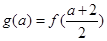
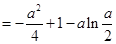 在
在 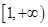 上单调递减,
上单调递减,
所以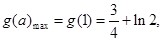 则
则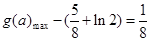
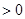 ,
,
因此存在实数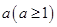 使
使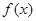 的最小值大于
的最小值大于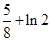 ,
,
故存在实数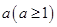 使
使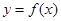 的图象与
的图象与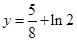 无公共点.
无公共点.
【解析】略

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目