题目内容
已知动圆S过点T(0,2)且被x轴截得的弦CD长为4。
(1)求动圆圆心S的轨迹E的方程;
(2)设P是直线l:y=x-2上任意一点,过P作轨迹E的切线PA,PB,A,B是切点,求证:直线AB恒过定点M;
(3)在(2)的条件下,过定点M作直线l:y=x-2的垂线,垂足为N,求证:MN是∠ANB的平分线。
(1)求动圆圆心S的轨迹E的方程;
(2)设P是直线l:y=x-2上任意一点,过P作轨迹E的切线PA,PB,A,B是切点,求证:直线AB恒过定点M;
(3)在(2)的条件下,过定点M作直线l:y=x-2的垂线,垂足为N,求证:MN是∠ANB的平分线。
解:(1)设S(x,y),根据题意,
|ST|2=|SC|2=22+|y|2,
即 。
。
(2)证明:设A(x1,y1),B(x2,y2)
所以
则PA: ,即
,即
设P(t,t-2),P在PA上
同理,P在PB上
故x1,x2是方程
的两根 ,
,



故恒过点(2,2)。
(3)证明:过点M所作垂线l1的方程为y-2=-(x-2) x+y-4=0,解出垂足N(3,1)
x+y-4=0,解出垂足N(3,1)
MN的斜率为-1,故倾斜角为
若AN,BN的斜率均存在,则设其分别为k1,k2,
对应的倾斜角分别为α,β,
要证MN是∠ANB的平分线,只要证∠ANM=∠BNM,
即 ,
,
即要证k1k2=1

设直线AB的斜率为k,则直线AB的方程为y= k(x-2)+2代入x2=4y,
得x2-4kx+8k-8=0,
∴x1+x2=4k,x1x2=8k-8
y1+y2=k(x1-2)+2+k(x2-2)+2 =4k2-4k+4,②
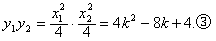
将②,③代入①,得

当 时,k1k2=1,当
时,k1k2=1,当 时,解得A,B两点的坐标分别为(-2,1),
时,解得A,B两点的坐标分别为(-2,1), ,
,
验证AN与BN的斜率一个不存在,一个为零,
即∠ANM=∠BNM,
即MN是∠ANB的平分线。
|ST|2=|SC|2=22+|y|2,
即
 。
。(2)证明:设A(x1,y1),B(x2,y2)

所以

则PA:
 ,即
,即
设P(t,t-2),P在PA上

同理,P在PB上

故x1,x2是方程

的两根
 ,
,


故恒过点(2,2)。
(3)证明:过点M所作垂线l1的方程为y-2=-(x-2)
 x+y-4=0,解出垂足N(3,1)
x+y-4=0,解出垂足N(3,1)MN的斜率为-1,故倾斜角为

若AN,BN的斜率均存在,则设其分别为k1,k2,
对应的倾斜角分别为α,β,
要证MN是∠ANB的平分线,只要证∠ANM=∠BNM,
即
 ,
,即要证k1k2=1

设直线AB的斜率为k,则直线AB的方程为y= k(x-2)+2代入x2=4y,
得x2-4kx+8k-8=0,
∴x1+x2=4k,x1x2=8k-8
y1+y2=k(x1-2)+2+k(x2-2)+2 =4k2-4k+4,②
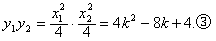
将②,③代入①,得

当
 时,k1k2=1,当
时,k1k2=1,当 时,解得A,B两点的坐标分别为(-2,1),
时,解得A,B两点的坐标分别为(-2,1), ,
,验证AN与BN的斜率一个不存在,一个为零,
即∠ANM=∠BNM,
即MN是∠ANB的平分线。

练习册系列答案
相关题目