题目内容
给出下列命题:①函数
 的一条对称轴是直线
的一条对称轴是直线
②已知函数
 ;
;③若α,β均为第一象限角,且α>β,则sinα>sinβ.
其中真命题的个数为( )
A.0
B.1
C.2
D.3
【答案】分析:①函数 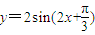 有一条对称轴方程是
有一条对称轴方程是 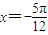 ,由正弦函数的性质直接求出对称轴方程比较即可;
,由正弦函数的性质直接求出对称轴方程比较即可;
②f(x)=min{sinx,cosx}知f(x)为正弦余弦的最小值,通过函数图象判断.
③根据正弦函数在第一象限的单调性直接判断.
解答:解:①函数 有一条对称轴方程是
有一条对称轴方程是 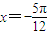 是正确命题,令
是正确命题,令 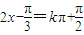 ,解得
,解得 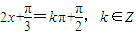 ,当k=-1时即得;
,当k=-1时即得;
②已知函数f(x)=min{sinx,cosx},则f(x)的值域为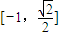 ;
;
根据正弦函数余弦函数图象易知,两者最小值为-1,最小值中最大为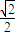
故正确
③若α,β均为第一象限角,且α>β,则sinα<sinβ.
因为第一象限正弦函数不具有单调性,显然不正确.
故选C.
点评:本题考查余弦函数的对称性,以及余弦函数的图象.通过对三个选项的分析分别判断,本题为中档题.
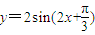 有一条对称轴方程是
有一条对称轴方程是 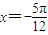 ,由正弦函数的性质直接求出对称轴方程比较即可;
,由正弦函数的性质直接求出对称轴方程比较即可;②f(x)=min{sinx,cosx}知f(x)为正弦余弦的最小值,通过函数图象判断.
③根据正弦函数在第一象限的单调性直接判断.
解答:解:①函数
 有一条对称轴方程是
有一条对称轴方程是 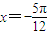 是正确命题,令
是正确命题,令 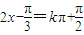 ,解得
,解得 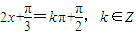 ,当k=-1时即得;
,当k=-1时即得;②已知函数f(x)=min{sinx,cosx},则f(x)的值域为
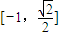 ;
;根据正弦函数余弦函数图象易知,两者最小值为-1,最小值中最大为
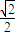
故正确
③若α,β均为第一象限角,且α>β,则sinα<sinβ.
因为第一象限正弦函数不具有单调性,显然不正确.
故选C.
点评:本题考查余弦函数的对称性,以及余弦函数的图象.通过对三个选项的分析分别判断,本题为中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目