题目内容
已知椭圆 :
: 的左焦点为
的左焦点为 ,右焦点为
,右焦点为 .
.

(Ⅰ)设直线 过点
过点 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线 垂直
垂直 于点P,线段
于点P,线段 的垂直平分线交
的垂直平分线交 于点M,求点M的轨迹
于点M,求点M的轨迹 的方程;
的方程;
(Ⅱ)设 为坐标原点,取曲线
为坐标原点,取曲线 上不同于
上不同于 的点
的点 ,以
,以 为直径作圆与
为直径作圆与 相交另外一点
相交另外一点 ,求该圆的面积最小时点
,求该圆的面积最小时点 的坐标.
的坐标.
【答案】
(Ⅰ)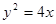 (Ⅱ)
(Ⅱ)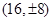 .
.
【解析】
试题分析:(Ⅰ) 利用抛物线的定义“到定点的距离等于到定直线的距离”来求;(Ⅱ) 直线与抛物线相交,联立消元,设点代入化简,利用基本不等式求最值.
试题解析:(I)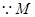 在线段
在线段 的垂直平分线上,∴| MP | = | M
的垂直平分线上,∴| MP | = | M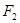 |
|
故动点M到定直线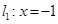 的距离等于它到定点
的距离等于它到定点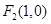 的距离
的距离
因此动点M的轨迹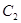 是以
是以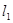 为准线,
为准线,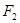 为焦点的抛物线,
为焦点的抛物线,
所以点M的轨迹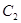 的方程为
的方程为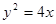
(II)因为以OS为直径的圆与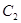 相交于点R,
相交于点R,
所以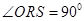 ,即
,即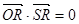
设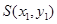 ,
, ,则
,则
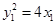 ,
,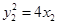 ,
,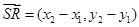 ,
,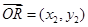
所以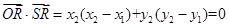 ,即
,即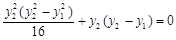
∵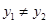 ,
,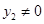 ,∴
,∴
故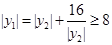 ,当且仅当
,当且仅当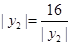 ,即
,即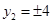 时等号成立
时等号成立
当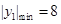 时,
时,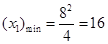 ,圆的直径
,圆的直径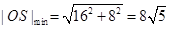 ,
,
这时点S的坐标为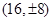 .
.
考点:抛物线的定义,向量的坐标运算,基本不等式,坐标表示等,考查了学生的综合化简计算能力.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目


 的左焦点为
的左焦点为 (-1,0),离心率为
(-1,0),离心率为 ,过点
,过点 与椭圆C交于
与椭圆C交于 两点.
两点. 轴交于点G,求点G横坐标的取值范围.
轴交于点G,求点G横坐标的取值范围.