题目内容
 (2010•聊城一模)如图,在三棱锥P-ABC中,已知PC⊥平面ABC,点C在平面PBA内的射影D在直线PB上.
(2010•聊城一模)如图,在三棱锥P-ABC中,已知PC⊥平面ABC,点C在平面PBA内的射影D在直线PB上.(1)求证:AB⊥平面PBC;
(2)设AB=BC,直线PA与平面ABC所成的角为45°,求异面直线AP与BC所成的角;
(3)在(2)的条件下,求二面角C-PA-B的余弦值.
分析:(1)要证AB⊥平面PBC,可证AB⊥PC,AB⊥CD,由线面垂直的性质及点在面内射影的定义可证明;
(2)由PC⊥平面ABC,知∠PAC=45°,设AB=BC=1,则PC=AC=
,以B为原点建立空间直角坐标系,求出点B、A、C、P坐标,进而写出
、
的坐标,则异面直线AP与BC所成的角可转化为
、
的夹角计算,注意其与异面角间的关系;
(3)取AC的中点E,连结BE,易证
是平面PAC的一个法向量.设平面PAB的一个法向量为
=(x,y,z),由
⊥
,
⊥
可求得
,从而二面角C-PA-B的余弦值可转化为两法向量的夹角余弦值,注意向量的夹角与二面角夹角的关系;
(2)由PC⊥平面ABC,知∠PAC=45°,设AB=BC=1,则PC=AC=
| 2 |
| AP |
| BC |
| AP |
| BC |
(3)取AC的中点E,连结BE,易证
| BE |
| n |
| n |
| BA |
| n |
| AP |
| n |
解答:证明: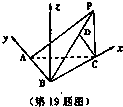 (1)由于PC⊥平面ABC,AB?平面ABC,所以AB⊥PC,
(1)由于PC⊥平面ABC,AB?平面ABC,所以AB⊥PC,
由于点C在平面PBA内的射影在直线PB上,
所以CD⊥平面PAB.
又因为AB?平面PBA,所以AB⊥CD.
因此AB⊥平面PCB.
解:(2)因为PC⊥平面ABC,
所以∠PAC为直线PC与平面ABC所成的角,
于是∠PAC=45°,设AB=BC=1,则PC=AC=
,
以B为原点建立如图所示空间直角坐标系,
则B(0,0,0),A(0,1,0),C(1,0,0),P(1,0,
),
=(1,-1,
),
=(1,0,0),
=(0,1,0),
因为cos<
,
>=
=
,
所以异面直线AP与BC所成的角为60°;
(3)取AC的中点E,连结BE,则
=(
,
,0).
因为AB=BC,所以BE⊥AC.
又因为平面PCA⊥平面ABC,所以BE⊥平面PAC.
因此,
是平面PAC的一个法向量.
设平面PAB的一个法向量为
=(x,y,z),
则由
,得
,取z=1,得
,
因此,
=(-
,0,1),
于是cos<
,
>=
=
=-
.
又因为二面角C-PA-B为锐角,故所求二面角的余弦值为
.
 (1)由于PC⊥平面ABC,AB?平面ABC,所以AB⊥PC,
(1)由于PC⊥平面ABC,AB?平面ABC,所以AB⊥PC,由于点C在平面PBA内的射影在直线PB上,
所以CD⊥平面PAB.
又因为AB?平面PBA,所以AB⊥CD.
因此AB⊥平面PCB.
解:(2)因为PC⊥平面ABC,
所以∠PAC为直线PC与平面ABC所成的角,
于是∠PAC=45°,设AB=BC=1,则PC=AC=
| 2 |
以B为原点建立如图所示空间直角坐标系,
则B(0,0,0),A(0,1,0),C(1,0,0),P(1,0,
| 2 |
| AP |
| 2 |
| BC |
| BA |
因为cos<
| AP |
| BC |
| ||||
|
|
| 1 |
| 2 |
所以异面直线AP与BC所成的角为60°;
(3)取AC的中点E,连结BE,则
| BE |
| 1 |
| 2 |
| 1 |
| 2 |
因为AB=BC,所以BE⊥AC.
又因为平面PCA⊥平面ABC,所以BE⊥平面PAC.
因此,
| BE |
设平面PAB的一个法向量为
| n |
则由
|
|
|
因此,
| n |
| 2 |
于是cos<
| n |
| BE |
| ||||
|
|
-
| ||||||
|
| ||
| 3 |
又因为二面角C-PA-B为锐角,故所求二面角的余弦值为
| ||
| 3 |
点评:本题考查线面垂直、异面直线及其所成角、二面角,考查空间向量在立体几何中的应用.

练习册系列答案
相关题目
 (2010•聊城一模)如图,在直角梯形ABEF中,将四边形DCEF沿CD折起,使∠FDA=60°,得到一个空间几何体如图所示.
(2010•聊城一模)如图,在直角梯形ABEF中,将四边形DCEF沿CD折起,使∠FDA=60°,得到一个空间几何体如图所示.