题目内容
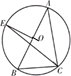
（2011•南通一模） 选修4-1：几何证明选讲锐角三角形ABC内接于⊙O，∠ABC=60°，∠BAC=40°．作OE⊥AB交劣弧
 | AB |
分析：连接OC．如图所示．由∠ABC=60°，∠BAC=40°，利用三角形的内角和定理可得∠ACB=80°．由OE⊥AB，利用垂径定理及其推论可得E为
的中点，
和
的度数均为80°．进而得到∠EOC=80°+80°=160°．利用等腰三角形即可得出∠OEC=10°．
|
| AB |
|
| BE |
|
| BC |
解答：解：连接OC．如图所示，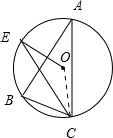
∵∠ABC=60°，∠BAC=40°，∴∠ACB=80°．
∵OE⊥AB，
∴E为
的中点，∴
和
的度数均为80°．
∴∠EOC=80°+80°=160°．
∴∠OEC=10°．
∵∠ABC=60°，∠BAC=40°，∴∠ACB=80°．
∵OE⊥AB，
∴E为
|
| AB |
|
| BE |
|
| BC |
∴∠EOC=80°+80°=160°．
∴∠OEC=10°．
点评：熟练掌握三角形的内角和定理、垂径定理及其推论、等腰三角形的性质是解题的关键．
练习册系列答案
相关题目