题目内容
设椭圆的两个焦点为F1(![]() ,0)、F2(
,0)、F2(![]() ,0),P为此椭圆上的一点,且|PF1|+|PF2|=6.
,0),P为此椭圆上的一点,且|PF1|+|PF2|=6.
若P、F1、F2是一直角三角形的三个顶点,|PF1|>|PF2|,求![]() 的值.
的值.
答案:
解析:
提示:
解析:
|
解:由题设知|PF1|+|PF2|=6,|F1F2|= 若∠PF2F1为直角,则|PF1|2=|PF2|2+|F1F2|2, 即|PF1|2=(6-|PF1|)2+20. ∴|PF1|= 若∠F1PF2为直角,则|F1F2|2=|PF1|2+|PF2|2, 即20=|PF1|2+(6-|PF1|)2, ∴|PF1|=4,|PF2|=2.∴ |
提示:
|
涉及椭圆的焦点和椭圆上一点之间的距离问题,常用椭圆定义来解决,由于△PF1F2的直角顶点未给出,故要讨论后分别求解,由|PF1|>|PF2|知∠PF1F2不可能为直角. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
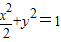 的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B.
的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线与圆O相切并与椭圆交于不同的两点A,B. ,求直线l的方程;
,求直线l的方程; ,求三角形OAB面积的取值范围.
,求三角形OAB面积的取值范围.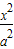 +
+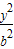 =1(a>b>0)的两个焦点为F1、F2,短轴两端点B1、B2,已知F1、F2、B1、B2四点共圆,且点N(0,3)到椭圆上的点最远距离为5
=1(a>b>0)的两个焦点为F1、F2,短轴两端点B1、B2,已知F1、F2、B1、B2四点共圆,且点N(0,3)到椭圆上的点最远距离为5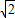 .
.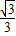 )、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
)、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.