题目内容

已知双曲线C的中心是原点，右焦点为F，一条渐近线m:,设过点A的直线l的方向向量。

（1）　　　 求双曲线C的方程；　

（2）　　　 若过原点的直线，且a与l的距离为，求K的值；

（3）　　　 证明：当时，在双曲线C的右支上不存在点Q，使之到直线l的距离为.

【解】（1）设双曲线的方程为

   ，解额双曲线的方程为

（2）直线，直线

由题意，得，解得

（3）【证法一】设过原点且平行于的直线

则直线与的距离当时，

又双曲线的渐近线为

  双曲线的右支在直线的右下方，

  双曲线右支上的任意点到直线的距离大于。

故在双曲线的右支上不存在点，使之到直线的距离为

【证法二】假设双曲线右支上存在点到直线的距离为，

则

由（1）得

设，

当时，；

将代入（2）得

，

  方程不存在正根，即假设不成立，

故在双曲线的右支上不存在点，使之到直线的距离为

练习册系列答案
相关题目
已知双曲线C的中心是原点，右焦点为F(
3
，0)，一条渐近线m：x+
2
y=0，设过点A（-3
2
，0）的直线l的方向向量e=（1，k），
（1）求双曲线C的方程；
（2）若过原点的直线a∥l，且a与l的距离为
6
，求k的值；
（3）证明：当k＞
2
2
时，在双曲线C的右支上不存在点Q，使之到直线l的距离为
6
．
已知双曲线C的中心是原点，右焦点为F(
3
，0)，焦点到一条渐近线距离为
2
，则双曲线C的渐近线方程为（　　）
A、y=±
3
x
B、y=±x
C、x=±
2
2
y
D、x=±
2
y

（本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分4分，第3小题满分8分。

已知双曲线C的中心是原点，右焦点为F，一条渐近线m:，设过点A的直线l的方向向量。

（1）求双曲线C的方程；

（2）若过原点的直线，且a与l的距离为，求K的值；

（3）证明：当时，在双曲线C的右支上不存在点Q，使之到直线l的距离为。

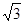（12分）已知双曲线C的中心是原点，右焦点为F(,0)，一条渐近线m:x+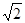y=0，设过点A(－3,0)的直线l

（1）求双曲线C的方程；

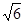（2）若过原点的直线a∥l，且a与l的距离为，求k的值；

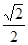（3）证明：当k＞时，在双曲线C的右支上不存在点Q，使之到直线l的距离为.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网