题目内容
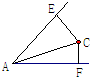
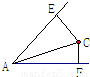
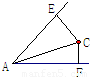
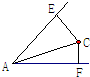 如图,∠A=60°,∠A内的点C到角的两边的距离分别为5和2,则AC的长为
如图,∠A=60°,∠A内的点C到角的两边的距离分别为5和2,则AC的长为分析:延长FC,与AE交于点B,由∠BAF为60°,CF垂直于AF,可得∠ABF为30°,又CE垂直于AB,在直角三角形BEC中,根据30°角所对的直角边等于斜边的一半可由EC的长求出BC的长,进而求出BF的长,然后在直角三角形ABF中,利用锐角的正切函数定义求出AF的长,再在直角三角形ACF中,由CF和AF的长,利用勾股定理即可求出AC的长.
解答: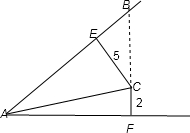
解:延长FC,延长线与AE交于点B,
由∠EAF=60°,CF⊥AF,
∴∠ABF=30°,又CE⊥AB,即∠BEC=90°,且CE=5,
∴BC=2EC=10,又CF=2,
∴BF=BC+CF=10+2=12,
在直角三角形ABF中,
tan∠ABF=tan30°=
,
∴AF=BFtan30°=12×
=4
,
在直角三角形ACF中,根据勾股定理得:
AC=
=2
.
故答案为:2

解:延长FC,延长线与AE交于点B,
由∠EAF=60°,CF⊥AF,
∴∠ABF=30°,又CE⊥AB,即∠BEC=90°,且CE=5,
∴BC=2EC=10,又CF=2,
∴BF=BC+CF=10+2=12,
在直角三角形ABF中,
tan∠ABF=tan30°=
| AF |
| BF |
∴AF=BFtan30°=12×
| ||
| 3 |
| 3 |
在直角三角形ACF中,根据勾股定理得:
AC=
| AF2+CF2 |
| 13 |
故答案为:2
| 13 |
点评:此题考查了解三角形的运算,涉及的知识有:直角三角形中30°角所对的直角边等于斜边的一半的性质,锐角三角函数以及勾股定理,其中作出辅助线是本题的突破点,熟练掌握直角三角形的性质及锐角三角函数定义是解本题的关键.

练习册系列答案
相关题目
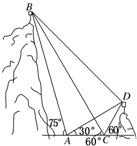 如图,A、B、C、D都在同一个与水平面垂直的平面内,B、D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1 km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01 km,
如图,A、B、C、D都在同一个与水平面垂直的平面内,B、D为两岛上的两座灯塔的塔顶.测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1 km.试探究图中B,D间距离与另外哪两点间距离相等,然后求B,D的距离(计算结果精确到0.01 km,