题目内容
已知边长为1的正方形ABCD中,AB与x轴正半轴成30°角.求点B和点D的坐标和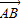 与
与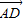 的坐标.
的坐标.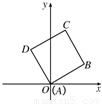
【答案】分析:根据题意,得∠BAx=30°,∠DAx=90°+30°=120°.由此结合三角函数的定义,算出点B、D两点的坐标,进而可得到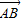 与
与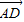 的坐标.
的坐标.
解答:解:由题意,点A在原点,AB与x轴正半轴成30°
可得∠BAx=30°,∠DAx=90°+30°=120°.
设B(x1,y1),D(x2,y2).
则x1=|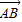 |cos 30°=1×
|cos 30°=1×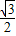 =
=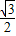 ,y1=|
,y1=|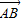 |sin 30°=1×
|sin 30°=1× =
= ,
,
∴B(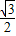 ,
, ).
).
同理可得x2=|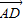 |cos 120°=1×(-
|cos 120°=1×(- )=-
)=- ,y2=|
,y2=|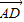 |sin 120°=1×
|sin 120°=1×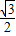 =
=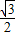 ,
,
∴D(- ,
,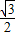 ).
).
∴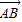 =(
=( ,
, ),
),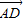 =(-
=(- ,
,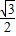 ).
).
点评:本题将正方形放置于坐标系中,求点B和点D的坐标和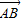 与
与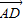 的坐标.着重考查了正方形的性质、向量的坐标运算等知识,属于基础题.
的坐标.着重考查了正方形的性质、向量的坐标运算等知识,属于基础题.
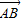 与
与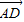 的坐标.
的坐标.解答:解:由题意,点A在原点,AB与x轴正半轴成30°
可得∠BAx=30°,∠DAx=90°+30°=120°.
设B(x1,y1),D(x2,y2).
则x1=|
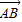 |cos 30°=1×
|cos 30°=1×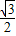 =
=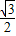 ,y1=|
,y1=|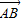 |sin 30°=1×
|sin 30°=1× =
= ,
,∴B(
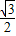 ,
, ).
).同理可得x2=|
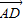 |cos 120°=1×(-
|cos 120°=1×(- )=-
)=- ,y2=|
,y2=|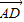 |sin 120°=1×
|sin 120°=1×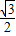 =
=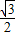 ,
,∴D(-
 ,
,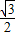 ).
).∴
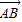 =(
=( ,
, ),
),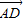 =(-
=(- ,
,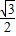 ).
).点评:本题将正方形放置于坐标系中,求点B和点D的坐标和
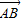 与
与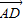 的坐标.着重考查了正方形的性质、向量的坐标运算等知识,属于基础题.
的坐标.着重考查了正方形的性质、向量的坐标运算等知识,属于基础题. 
练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
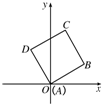 已知边长为1的正方形ABCD中,AB与x轴正半轴成30°角.求点B和点D的坐标和
已知边长为1的正方形ABCD中,AB与x轴正半轴成30°角.求点B和点D的坐标和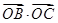 的最大值是(
)
的最大值是(
)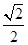 C.2 D.
C.2 D.