题目内容
如图,在四面体ABCD中,截面PQMN是正方形,则下列命题中错误的是( )
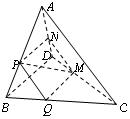
A.AC⊥BD B.AC∥平面PQMN
C.AC=BD D.异面直线PM与BD所成的角为45°
C
解析:
由PQ∥AC,QM∥BD,PQ⊥QM,可得AC⊥BD,所以A答案正确;由PQ∥AC可得AC∥平面PQMN,所以B答案正确;因为异面直线PM与BD所成的角等于PM与PN所成的角,即45°,故D答案正确。

练习册系列答案
相关题目
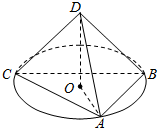 如图,在四面体ABCD中,DA=DB=DC=1,且DA,DB,DC两两互相垂直,点O是△ABC的中心,将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与BC所成角的余弦值的取值范围是( )
如图,在四面体ABCD中,DA=DB=DC=1,且DA,DB,DC两两互相垂直,点O是△ABC的中心,将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与BC所成角的余弦值的取值范围是( )A、[0,
| ||||
B、[0,
| ||||
C、[0,
| ||||
D、[0,
|
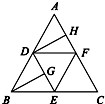 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为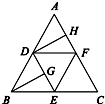 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为( )
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为( )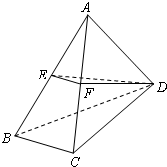 如图,在四面体ABCD中,BC⊥面ACD,DA=DC,E、F分别为AB、AC的中点.
如图,在四面体ABCD中,BC⊥面ACD,DA=DC,E、F分别为AB、AC的中点.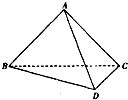 (2009•武汉模拟)如图,在四面体A-BCD中,
(2009•武汉模拟)如图,在四面体A-BCD中,