题目内容
已知A,B,C,D四点的坐标分别为A(-1,0),B(1,0),C(0,1),D(2,0),P是线段CD上的任意一点,则
•
的最小值是
| AP |
| BP |
-
| 1 |
| 5 |
-
.| 1 |
| 5 |
分析:由题意可得:线段CD的方程为:x+2y-2=0,设点p(a,b),则b=1-
a,并且a∈[0,2],结合题意可得:
=(a+1,b),
=(a-1,b),所以
•
=
a2-a,a∈[0,2],再由二次函数的性质可得答案.
| 1 |
| 2 |
| AP |
| BP |
| AP |
| BP |
| 5 |
| 4 |
解答:解:因为C(0,1),D(2,0),
所以线段CD的方程为:x+2y-2=0,
设点p(a,b),则b=1-
a,并且a∈[0,2],
因为A(-1,0),B(1,0),
所以
=(a+1,b),
=(a-1,b),
所以
•
=a2-1+b2=a2-1+(1-
a)2=
a2-a,a∈[0,2]
所以由二次函数的性质可得:当a=
时
•
由最小值-
.
故答案为:-
.
所以线段CD的方程为:x+2y-2=0,
设点p(a,b),则b=1-
| 1 |
| 2 |
因为A(-1,0),B(1,0),
所以
| AP |
| BP |
所以
| AP |
| BP |
| 1 |
| 2 |
| 5 |
| 4 |
所以由二次函数的性质可得:当a=
| 2 |
| 5 |
| AP |
| BP |
| 1 |
| 5 |
故答案为:-
| 1 |
| 5 |
点评:本题主要考查向量的数量积运算,以及二次函数定区间上求最值问题,此题属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
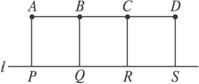
 如图,A、B、C、D是某煤矿的四个采煤点,l是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形.已知A、B、C、D四个采煤点每天的采煤量之比约为5:1:2:3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P、Q、R、S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在( )
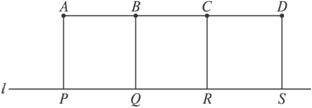
如图,A、B、C、D是某煤矿的四个采煤点,l是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形.已知A、B、C、D四个采煤点每天的采煤量之比约为5:1:2:3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P、Q、R、S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在( )