题目内容
在函数y=sin|x|，y=|sinx|，y=sin（2x+
）中，最小正周期为π的函数有 个．
| 2π | 3 |
分析：利用周期函数的概念，对y=sin|x|，y=|sinx|，y=sin（2x+
）的周期情况逐个分析即可．
| 2π |
| 3 |
解答：解：∵y=sin|x|不是周期函数，
令y=f（x）=|sinx|，
则f（x+π）=|sin（x+π）|=|-sinx|=|sinx|=f（x），
∴y=|sinx|是最小正周期为π的函数；
又y=sin（2x+
）的最小正周期T=
=π，
∴y=sin（2x+
）是最小正周期为π的函数，
∴以上三个函数中，最小正周期为π的函数有2个，
故答案为：2．
令y=f（x）=|sinx|，
则f（x+π）=|sin（x+π）|=|-sinx|=|sinx|=f（x），
∴y=|sinx|是最小正周期为π的函数；
又y=sin（2x+
| 2π |
| 3 |
| 2π |
| 2 |
∴y=sin（2x+
| 2π |
| 3 |
∴以上三个函数中，最小正周期为π的函数有2个，
故答案为：2．
点评：本题考查三角函数的周期性及其求法，考查分析与运算能力，属于中档题．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
在函数y=sin|x|、y=|sinx|、y=sin(2x+
)、y=cos(2x+
)中，最小正周期为π的函数的个数为（ ）
| 2π |
| 3 |
| 2π |
| 3 |
| A、1个 | B、2个* | C、3个 | D、4个 |
、
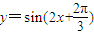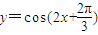中，最小正周期为π的函数的个数为（ ）