题目内容
已知定义在R上的函数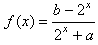 是奇函数,
是奇函数,
(1)求a,b的值;
(2)判断f(x)的单调性,并用单调性定义证明;
(3)若对任意的t∈R,不等式f(t-2t2)+f(-k)>0恒成立,求实数k的取值范围。
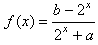 是奇函数,
是奇函数,(1)求a,b的值;
(2)判断f(x)的单调性,并用单调性定义证明;
(3)若对任意的t∈R,不等式f(t-2t2)+f(-k)>0恒成立,求实数k的取值范围。
解:(1)∵f(x)是定义在R上的奇函数,
∴ ,
,
∴b=1, ,
,
 ,
,
∴ 对一切实数x都成立,
对一切实数x都成立,
∴a=1,
∴a=b=1;
(2) ,f(x)在R上是减函数,
,f(x)在R上是减函数,
证明:设 ,
,
则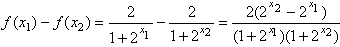 ,
,
 ,
,
∴ ,
,
∴ ,
,
∴f(x)在R上是减函数。
(3)不等式 ,
,
又f(x)是R上的减函数,
∴ ,
,
 对t∈R恒成立,
对t∈R恒成立,
∴ 。
。
∴
 ,
,∴b=1,
 ,
, ,
,∴
 对一切实数x都成立,
对一切实数x都成立,∴a=1,
∴a=b=1;
(2)
 ,f(x)在R上是减函数,
,f(x)在R上是减函数,证明:设
 ,
,则
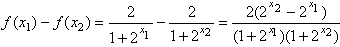 ,
, ,
,∴
 ,
,∴
 ,
,∴f(x)在R上是减函数。
(3)不等式
 ,
,又f(x)是R上的减函数,
∴
 ,
, 对t∈R恒成立,
对t∈R恒成立,∴
 。
。
练习册系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |