题目内容
一椭圆其中心在原点,焦点在同一坐标轴上,焦距为2| 13 |
分析:首先根据焦点分别在x轴、y轴上进行分类,不妨先设焦点在x轴上的椭圆、双曲线的标准方程,然后根据题意与椭圆、双曲线的性质列方程组,再解方程组求得焦点在x轴上的椭圆、双曲线的标准方程,最后把焦点在y轴上的椭圆、双曲线的标准方程补充上即可.
解答:解:若椭圆、双曲线的焦点在x轴上,则设椭圆、双曲线的标准方程分别为
+
=1、
-
=1,
由题意得
解得a1=7,a2=3,b1=6,b2=2,
所以焦点在x轴上的椭圆、双曲线的标准方程分别为
+
=1和
-
=1;
同理焦点在y轴上的椭圆、双曲线的标准方程分别为
+
=1和
-
=1.
| x2 |
| a12 |
| y2 |
| b12 |
| x2 |
| a22 |
| y2 |
| b22 |
由题意得
|
解得a1=7,a2=3,b1=6,b2=2,
所以焦点在x轴上的椭圆、双曲线的标准方程分别为
| x2 |
| 49 |
| y2 |
| 36 |
| x2 |
| 9 |
| y2 |
| 4 |
同理焦点在y轴上的椭圆、双曲线的标准方程分别为
| y2 |
| 49 |
| x2 |
| 36 |
| y2 |
| 9 |
| x2 |
| 4 |
点评:本题主要考查椭圆、双曲线的标准方程.

练习册系列答案
相关题目
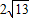 ,一双曲线和这椭圆有公共焦点,且双曲线的半实轴比椭圆的长半轴长小4,且双曲线的离心率与椭圆的离心率之比为7:3,求椭圆和双曲线的方程.
,一双曲线和这椭圆有公共焦点,且双曲线的半实轴比椭圆的长半轴长小4,且双曲线的离心率与椭圆的离心率之比为7:3,求椭圆和双曲线的方程.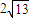 ,一双曲线和这椭圆有公共焦点,且双曲线的半实轴比椭圆的长半轴长小4,且双曲线的离心率与椭圆的离心率之比为7:3,求椭圆和双曲线的方程.
,一双曲线和这椭圆有公共焦点,且双曲线的半实轴比椭圆的长半轴长小4,且双曲线的离心率与椭圆的离心率之比为7:3,求椭圆和双曲线的方程.