题目内容
已知a,b,c为的三内角A,B,C的对边,若a=1,b=
,A+C=2B,
(1)求sinA的值.
(2)求△ABC的面积.
| 3 |
(1)求sinA的值.
(2)求△ABC的面积.
分析:(1)根据A+C=2B结合三角形内角和定理,算出B=60°,再用正弦定理即可算出sinA的值;
(2)根据三角形大边对大角,得到A<60°,结合sinA=
,可得A=30°,因此△ABC是直角三角形且C为直角,由此结合三角形面积公式即可算出△ABC的面积.
(2)根据三角形大边对大角,得到A<60°,结合sinA=
| 1 |
| 2 |
解答:解:(1)∵△ABC中,A+C=2B且A+B+C=180°,∴B=60°
∵a=1,b=
,
∴由
=
,得sinA=
=
=
;
(2)∵a<b,B=60°,可得A<60°
∴由sinA=
,可得A=30°,C=180°-(A+B)=90°
因此,△ABC是以C为直角顶点的直角三角形
∴△ABC的面积S=
ab=
.
∵a=1,b=
| 3 |
∴由
| a |
| sinA |
| b |
| sinB |
| asinB |
| b |
| 1×sin60° | ||
|
| 1 |
| 2 |
(2)∵a<b,B=60°,可得A<60°
∴由sinA=
| 1 |
| 2 |
因此,△ABC是以C为直角顶点的直角三角形
∴△ABC的面积S=
| 1 |
| 2 |
| ||
| 2 |
点评:本题给出△ABC两边之值和其中一边的对角,求另一边的对角并求三角形面积,着重考查了利用正余弦定理解三角形、三角形面积公式等知识点,属于基础题.

练习册系列答案
相关题目
 的三个内角且向量
的三个内角且向量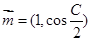 与
与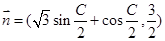 共线.
共线.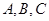 的对边分别是
的对边分别是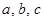 ,且满足
,且满足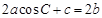 ,试判断
,试判断
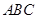 的形状.
的形状.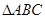 的三个内角,他们的对边分别为a、b、c,且
的三个内角,他们的对边分别为a、b、c,且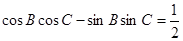 。
。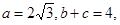 求bc的值,并求
求bc的值,并求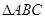 的三个内角且向量
的三个内角且向量 共线。
共线。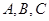 的对边分别是
的对边分别是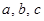 ,且满足
,且满足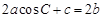 ,试判断
,试判断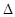
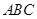 的形状.
的形状.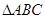 的三个内角且向量
的三个内角且向量 共线。
共线。 的对边分别是
的对边分别是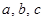 ,且满足
,且满足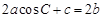 ,试判断
,试判断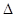
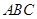 的形状.
的形状.