题目内容
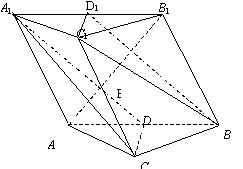
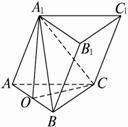
已知在斜三棱柱ABC—A1B1C1中,AC=BC,D为AB的中点,两底面分别与侧面ABB1A1
垂直,异面直线BC1与AB1互相垂直,
(1)求证:AB1⊥A1D;
(2)求证:AB1⊥平面A1CD;
(3)若CC1与平面AB B1 A1的距离为1,A1C![]() ,AB=6,求点A到平面A1CD的距离.
,AB=6,求点A到平面A1CD的距离.
答案:
解析:
解析:
证明:(1)取 又底面 又 (2)D为AB的中点,AC=BC, 由(1)AB1⊥A1D,而
(3)由CC1与平面AB B1 A1的距离为1, A1C 由(1)(2)AB1⊥A1D, AB1⊥平面A1CD,设AB1与A1D交于E,所以AE为A到平面A1CD的距离,
|

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目