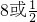题目内容
方程2lg（x-4）=lgx+lg2的解是（ ）
分析：利用对数的运算性质化对数方程为一般方程，求解后验根．
解答：解：由2lg（x-4）=lgx+lg2，
得lg（x-4）2=lg2x，即（x-4）2=2x，解得x1=2，x2=8．
当x=2时原方程无意义．
所以方程2lg（x-4）=lgx+lg2的解是8．
故选B．
得lg（x-4）2=lg2x，即（x-4）2=2x，解得x1=2，x2=8．
当x=2时原方程无意义．
所以方程2lg（x-4）=lgx+lg2的解是8．
故选B．
点评：本题考查了对数的运算性质，解答的关键是对数方程注意验根，是基础题也是易错题．
练习册系列答案
阶梯计算系列答案
相关题目
