题目内容
为了加快县域经济的发展,某县选择两乡镇作为龙头带动周边乡镇的发展,决定在这两个镇的周边修建环形高速公路,假设一个单位距离为10km,两镇的中心A、B相距8个单位距离,环形高速公路所在的曲线为E,且E上的点到A、B的距离之和为10个单位距离,在曲线E上建一个加油站M与一个收费站N,使M、N、B三点在一条直线上,并且AM+AN=12个单位距离.(1) 建立如图的直角坐标系,求曲线E的方程及M、N之间的距离有多少个单位距离;
(2)A、B之间有一条笔直公路Z与AB所在直线成45°,且与曲线E交于P,Q两点,该县招商部门引进外资在四边形PAQB区域开发旅游业,试问最大的开发区域是多少?(平方单位距离)
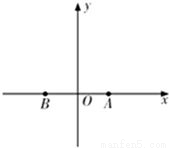
【答案】分析:(1)以AB为x轴,以A中点为原点O建立直角坐标系,设曲线上的点P(x,y),|PA|+|PB|=10>|AB|=8,动点轨迹为椭圆,且a=5,由此能够求出曲线E的方程.再由|AM|+|AN|+|BM|+|BN|=20,|AM|+|AN|=12,能够求出|MN|.
(2)将y=x+t代入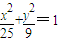 ,得34y2-18ty+9t2-25×9=0,设P(x1,y1),Q(x2,y2),再由根与系数的关系进行求解.
,得34y2-18ty+9t2-25×9=0,设P(x1,y1),Q(x2,y2),再由根与系数的关系进行求解.
解答:解:(1)以AB为x轴,以A中点为原点O建立直角坐标系,设曲线上的点P(x,y),
∵|PA|+|PB|=10>|AB|=8,
∴动点轨迹为椭圆,且a=5,c=4,b=3,
∴曲线E的方程是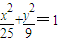 .
.
由|AM|+|AN|+|BM|+|BN|=20,|AM|+|AN|=12,
∴|MN|=8.
(2)将y=x+t代入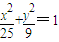 ,得34y2-18ty+9t2-25×9=0,
,得34y2-18ty+9t2-25×9=0,
设P(x1,y1),Q(x2,y2),则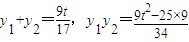 ,
,
|y1-y2|=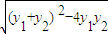 =
=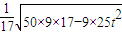 .
.
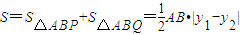
=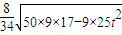 .
.
∴当t=0时,面积最大是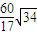 ,此是直线为l:y=x.
,此是直线为l:y=x.
点评:本题考查直线与圆的位置关系,解题时要认真审题,仔细解答,注意公式的合理选用
(2)将y=x+t代入
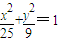 ,得34y2-18ty+9t2-25×9=0,设P(x1,y1),Q(x2,y2),再由根与系数的关系进行求解.
,得34y2-18ty+9t2-25×9=0,设P(x1,y1),Q(x2,y2),再由根与系数的关系进行求解.解答:解:(1)以AB为x轴,以A中点为原点O建立直角坐标系,设曲线上的点P(x,y),
∵|PA|+|PB|=10>|AB|=8,
∴动点轨迹为椭圆,且a=5,c=4,b=3,
∴曲线E的方程是
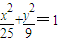 .
.由|AM|+|AN|+|BM|+|BN|=20,|AM|+|AN|=12,
∴|MN|=8.
(2)将y=x+t代入
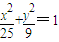 ,得34y2-18ty+9t2-25×9=0,
,得34y2-18ty+9t2-25×9=0,设P(x1,y1),Q(x2,y2),则
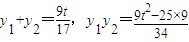 ,
,|y1-y2|=
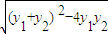 =
=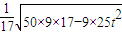 .
.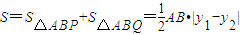
=
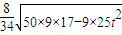 .
.∴当t=0时,面积最大是
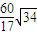 ,此是直线为l:y=x.
,此是直线为l:y=x.点评:本题考查直线与圆的位置关系,解题时要认真审题,仔细解答,注意公式的合理选用

练习册系列答案
相关题目
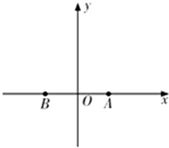 为了加快县域经济的发展,某县选择两乡镇作为龙头带动周边乡镇的发展,决定在这两个镇的周边修建环形高速公路,假设一个单位距离为10km,两镇的中心A、B相距8个单位距离,环形高速公路所在的曲线为E,且E上的点到A、B的距离之和为10个单位距离,在曲线E上建一个加油站M与一个收费站N,使M、N、B三点在一条直线上,并且AM+AN=12个单位距离.
为了加快县域经济的发展,某县选择两乡镇作为龙头带动周边乡镇的发展,决定在这两个镇的周边修建环形高速公路,假设一个单位距离为10km,两镇的中心A、B相距8个单位距离,环形高速公路所在的曲线为E,且E上的点到A、B的距离之和为10个单位距离,在曲线E上建一个加油站M与一个收费站N,使M、N、B三点在一条直线上,并且AM+AN=12个单位距离.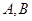 两城市作为龙头带动周边城市的发展,决定在
两城市作为龙头带动周边城市的发展,决定在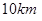 为一个单位距离,
为一个单位距离,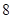 个单位距离,设城际轻轨所在的曲线为
个单位距离,设城际轻轨所在的曲线为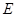 ,使轻轨
,使轻轨 个单位距离,
个单位距离,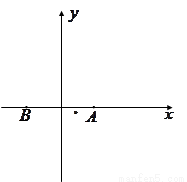
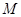 与一个收费站
与一个收费站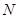 ,使
,使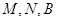 三点在一条直线上,并且
三点在一条直线上,并且 个单位距离,求
个单位距离,求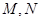 之间的距离有多少个单位距离?
之间的距离有多少个单位距离?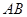 所在直线成
所在直线成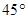 的笔直公路
的笔直公路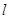 ,直线
,直线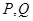 两点,求四边形
两点,求四边形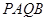 的面积的最大值.
的面积的最大值.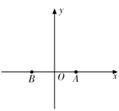 (1) 建立如图的直角坐标系,求曲线
(1) 建立如图的直角坐标系,求曲线