题目内容
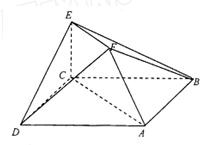
在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.(Ⅰ)求点A到平面BDE的距离;
(Ⅱ)求二面角B-ED-A的正切值.
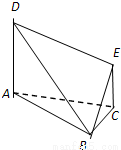
【答案】分析:(I)设点A到平面BDE的距离为h,然后根据VB-ADE=VA-BDE建立等式关系,求出h,即为点A到平面BDE的距离;
(II)取AC的中点M,连接BM,过M作MN⊥DE,交DE于N,连接BN,易知∠BNM是所求二面角的平面角,然后设AC、DE的延长线相交于点P,根据△MNP∽△DAP求出MN,可求出
二面角B-ED-A的正切值.
解答:解: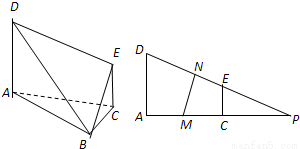 (Ⅰ)∵DE=BE=
(Ⅰ)∵DE=BE= ,BD=2
,BD=2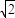 ,
,
∴S△BDE=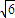 ,设点A到平面BDE的距离为h.
,设点A到平面BDE的距离为h.
又∵S△ABC=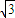 ,VB-ADE=VA-BDE
,VB-ADE=VA-BDE
∴ •
•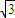 •2=
•2= •
•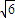 •h∴h=
•h∴h=
即点A到平面BDE的距离为 . …(6分)
. …(6分)
(Ⅱ)∵DA⊥平面ABC,∴平面DACE⊥平面ABC
取AC的中点M,连接BM,则BM⊥AC,BM⊥平面DACE.
过M作MN⊥DE,交DE于N,连接BN,则BN⊥DE,∴∠BNM是所求二面角的平面角.
设AC、DE的延长线相交于点P,∵DA=2EC,∴CP=2由△MNP∽△DAP得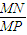 =
=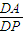 ,
,
MP=3,DA=2,DP=2 ,∴MN=
,∴MN=
又∵BM=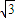 ,∴tan∠BNM=
,∴tan∠BNM=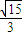 . …(12分)
. …(12分)
点评:本题主要考查了点到面的距离的度量以及二面角平面角的度量,考查空间想象能力、运算能力和推理论证能力,属于中档题.
(II)取AC的中点M,连接BM,过M作MN⊥DE,交DE于N,连接BN,易知∠BNM是所求二面角的平面角,然后设AC、DE的延长线相交于点P,根据△MNP∽△DAP求出MN,可求出
二面角B-ED-A的正切值.
解答:解:
 (Ⅰ)∵DE=BE=
(Ⅰ)∵DE=BE= ,BD=2
,BD=2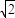 ,
,∴S△BDE=
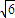 ,设点A到平面BDE的距离为h.
,设点A到平面BDE的距离为h.又∵S△ABC=
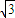 ,VB-ADE=VA-BDE
,VB-ADE=VA-BDE∴
 •
•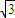 •2=
•2= •
•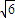 •h∴h=
•h∴h=
即点A到平面BDE的距离为
 . …(6分)
. …(6分)(Ⅱ)∵DA⊥平面ABC,∴平面DACE⊥平面ABC
取AC的中点M,连接BM,则BM⊥AC,BM⊥平面DACE.
过M作MN⊥DE,交DE于N,连接BN,则BN⊥DE,∴∠BNM是所求二面角的平面角.
设AC、DE的延长线相交于点P,∵DA=2EC,∴CP=2由△MNP∽△DAP得
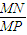 =
=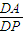 ,
,MP=3,DA=2,DP=2
 ,∴MN=
,∴MN=
又∵BM=
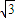 ,∴tan∠BNM=
,∴tan∠BNM=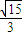 . …(12分)
. …(12分)点评:本题主要考查了点到面的距离的度量以及二面角平面角的度量,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=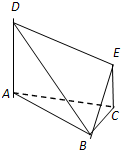 在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.
在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.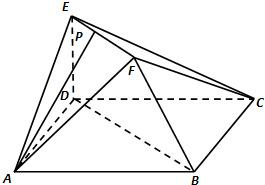 在如图所示的多面体中,已知正方形ABCD和
在如图所示的多面体中,已知正方形ABCD和 (2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点. 在如图所示的多面体中,AA1∥BB1,CC1⊥AC,CC1⊥BC.
在如图所示的多面体中,AA1∥BB1,CC1⊥AC,CC1⊥BC.