题目内容
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(1)(不等式选讲)已知函数f(x)=log2(|x-1|+|x-5|-a),当函数f(x)的定义域为R时,则实数a的取值范围为
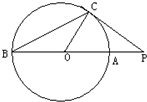
(2)(几何证明选讲)如图,AB是半圆O的直径,点C在半圆上,CD⊥AB,垂足为D,且AD=5DB,设∠COD=θ,则tanθ的值为
.
(3)(坐标系与参数方程)圆O1和圆O2的极坐标方程分别为ρ=4cosθ,ρ=-4sinθ,则经过两圆圆心的直线的直角坐标方程为
(1)(不等式选讲)已知函数f(x)=log2(|x-1|+|x-5|-a),当函数f(x)的定义域为R时,则实数a的取值范围为
(-∞,4)
(-∞,4)
(2)(几何证明选讲)如图,AB是半圆O的直径,点C在半圆上,CD⊥AB,垂足为D,且AD=5DB,设∠COD=θ,则tanθ的值为
| ||
| 2 |
| ||
| 2 |

(3)(坐标系与参数方程)圆O1和圆O2的极坐标方程分别为ρ=4cosθ,ρ=-4sinθ,则经过两圆圆心的直线的直角坐标方程为
y=x+2
y=x+2
.分析:(1)原问题?a<(|x-1|+|x-5|)min,通过分类讨论求出其最小值即可;
(2)利用圆的性质、射影定理及正切函数的定义即可得出;
(3)利用极坐标与直角坐标的互化公式、圆的标准方程及点斜式即可得出.
(2)利用圆的性质、射影定理及正切函数的定义即可得出;
(3)利用极坐标与直角坐标的互化公式、圆的标准方程及点斜式即可得出.
解答:解:(1)∵函数f(x)的定义域为R,∴|x-1|+|x-5|-a>0对于x∈R恒成立,
而|x-1|+|x-5|-a>0对于x∈R恒成立?a<(|x-1|+|x-5|)min.
令g(x)=|x-1|+|x-5|=
,可知g(x)min=4,∴a<4.
(2)连接AC,BC,∵AB是圆O的直径,∴AC⊥BC,又∵CD⊥AB,∴CD2=AD×DB,
∵AD=5DB,∴CD2=5DB2,∴CD=
DB.
∵r=
=3DB,∴OD=r-DB=2DB.
在Rt△OCD中,tanθ=
=
=
.
(3)圆O1的极坐标方程ρ=4cosθ可以化为ρ2=4ρcosθ,∴x2+y2=4x,∴(x-2)2+y2=4,∴圆心O1(2,0);
圆O2的极坐标方程ρ=-4sinθ可化为ρ2=4ρsinθ,∴x2+y2=4y,配方得x2+(y-2)2=4,∴圆心O2(0,2).
∴经过两圆圆心的直线的直角坐标方程为 y=
x+2,即y=x+2.
故答案分别为(-∞,4),
,y=x+2.
而|x-1|+|x-5|-a>0对于x∈R恒成立?a<(|x-1|+|x-5|)min.
令g(x)=|x-1|+|x-5|=
|
(2)连接AC,BC,∵AB是圆O的直径,∴AC⊥BC,又∵CD⊥AB,∴CD2=AD×DB,
∵AD=5DB,∴CD2=5DB2,∴CD=
| 5 |
∵r=
| AD+DB |
| 2 |
在Rt△OCD中,tanθ=
| CD |
| OD |
| ||
| 2DB |
| ||
| 2 |
(3)圆O1的极坐标方程ρ=4cosθ可以化为ρ2=4ρcosθ,∴x2+y2=4x,∴(x-2)2+y2=4,∴圆心O1(2,0);
圆O2的极坐标方程ρ=-4sinθ可化为ρ2=4ρsinθ,∴x2+y2=4y,配方得x2+(y-2)2=4,∴圆心O2(0,2).
∴经过两圆圆心的直线的直角坐标方程为 y=
| 0-2 |
| 2-0 |
故答案分别为(-∞,4),
| ||
| 2 |
点评:把问题正确等价转化,熟练掌握分类讨论的方法、圆的性质、射影定理及正切函数的定义、极坐标与直角坐标的互化公式、圆的标准方程及点斜式是解题的关键.

练习册系列答案
相关题目
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分) 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分) 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分) (2011•渭南三模)选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(2011•渭南三模)选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)