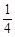Question

设a是从集合{1，2，3，4}中随机取出的一个数，b是从集合{1，2，3}中随机取出的一个数，构成一个基本事件（a，b）．记“这些基本事件中，满足log_ba≥1”为事件E，则E发生的概率是（　　）

• A、

  1

  2

• B、

  5

  12

• C、

  1

  3

• D、

  1

  4

Answer 1

分析：本题是一个古典概型，试验发生包含的事件是分别从两个集合中取两个数字，共有4×3种结果，满足条件的事件是满足log_ba≥1，可以列举出所有的事件，根据概率公式得到结果．

解答：解：由题意知本题是一个古典概型，
试验发生包含的事件是分别从两个集合中取两个数字，共有4×3=12种结果，
满足条件的事件是满足log_ba≥1，可以列举出所有的事件，
当b=2时，a=2，3，4，
当b=3时，a=3，4，共有3+2=5个，
∴根据古典概型的概率公式得到概率是

5

12

，
故选B．

点评：本题考查古典概型及其概率计算公式，考查分步计数原理和分类计数原理，利用这两个原理做出事件数，注意对数本身的使用范围．