题目内容
(理)已知极坐标系中,P (
,
),Q (2 ,
)两点,那么直线PQ与极轴所在直线所夹的锐角是
.
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
分析:首先由极坐标与直角坐标系转换公式
,把点A、B的极坐标转化为直角坐标,再在直角坐标系下求直线PQ与x轴所在直线所夹的锐角.
|
解答:解:由极坐标与直角坐标系转换公式
又A、B的极坐标分别为P (
,
),Q (2 ,
).
可得到P,Q的直角坐标分别为P(
,
),Q(1,
),
则直线PQ的斜率KPQ=
=-
直线PQ与x轴所在直线所夹的锐角
.
故答案为
.
|
又A、B的极坐标分别为P (
| 3 |
| π |
| 6 |
| π |
| 3 |
可得到P,Q的直角坐标分别为P(
| 3 |
| 2 |
| ||
| 2 |
| 3 |
则直线PQ的斜率KPQ=
| ||||||
1-
|
| 3 |
直线PQ与x轴所在直线所夹的锐角
| π |
| 3 |
故答案为
| π |
| 3 |
点评:此题主要考查极坐标与直角坐标系的转化公式的记忆与应用,有一定的计算量,在做题时需要很好的理解题意以便解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(理)在极坐标系中,已知曲线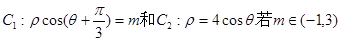 ,
,
则曲线C1与C2的位置关系是 ( )
| A.相切 | B.相交 | C.相离 | D.不确定 |
 ,
,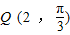 两点,那么直线PQ与极轴所在直线所夹的锐角是 .
两点,那么直线PQ与极轴所在直线所夹的锐角是 .