题目内容
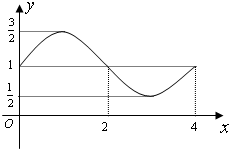 已知函数f(x)=Asin(ωx+φ)+B的一部分图象如图,那么f(x)的解析式以及S=f(0)+f(1)+f(2)…+f(2012)的值分别是
已知函数f(x)=Asin(ωx+φ)+B的一部分图象如图,那么f(x)的解析式以及S=f(0)+f(1)+f(2)…+f(2012)的值分别是
- A.
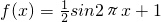 ,S=2011
,S=2011 - B.
 ,S=2013
,S=2013 - C.
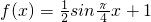 ,S=2012
,S=2012 - D.
 ,S=2012
,S=2012
B
分析:由函数的最值求出A和B,由周期求出ω,把特殊点(0,1)代入求出φ的值,从而求得函数的解析式为 f(x)= sin(
sin( x)+1.先求得求得f(0)+f(1)+f(2)+f(3)
x)+1.先求得求得f(0)+f(1)+f(2)+f(3)
=4,再利用函数的周期为4求得所求式子的值.
解答:由函数的图象可得B=1,A=1- =
= ,由函数的周期
,由函数的周期  =4,可得ω=
=4,可得ω= .
.
再把点(0,1)代入函数的解析式可得 sinφ+1=1,∴sinφ=0,∴φ=0.
sinφ+1=1,∴sinφ=0,∴φ=0.
故函数的解析式为 f(x)= sin(
sin( x)+1,求得f(0)+f(1)+f(2)+f(3)=4.
x)+1,求得f(0)+f(1)+f(2)+f(3)=4.
再由函数的周期为4可得S=f(0)+f(1)+f(2)…+f(2012)=503×[f(0)+f(1)+f(2)+f(3)]+f(1)=2013,
故选B.
点评:本题主要考查由函数y=Asin(ωx+?)的部分图象求解析式,由函数的最值求出A和B,由周期求出ω,把特殊点(0,1)代入求出φ的值,利用函数的周期性求式子的值,
属于中档题.
分析:由函数的最值求出A和B,由周期求出ω,把特殊点(0,1)代入求出φ的值,从而求得函数的解析式为 f(x)=
 sin(
sin( x)+1.先求得求得f(0)+f(1)+f(2)+f(3)
x)+1.先求得求得f(0)+f(1)+f(2)+f(3)=4,再利用函数的周期为4求得所求式子的值.
解答:由函数的图象可得B=1,A=1-
 =
= ,由函数的周期
,由函数的周期  =4,可得ω=
=4,可得ω= .
.再把点(0,1)代入函数的解析式可得
 sinφ+1=1,∴sinφ=0,∴φ=0.
sinφ+1=1,∴sinφ=0,∴φ=0.故函数的解析式为 f(x)=
 sin(
sin( x)+1,求得f(0)+f(1)+f(2)+f(3)=4.
x)+1,求得f(0)+f(1)+f(2)+f(3)=4.再由函数的周期为4可得S=f(0)+f(1)+f(2)…+f(2012)=503×[f(0)+f(1)+f(2)+f(3)]+f(1)=2013,
故选B.
点评:本题主要考查由函数y=Asin(ωx+?)的部分图象求解析式,由函数的最值求出A和B,由周期求出ω,把特殊点(0,1)代入求出φ的值,利用函数的周期性求式子的值,
属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目