题目内容
已知函数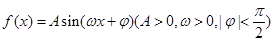 的部分图象如图所示.
的部分图象如图所示.
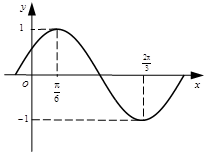
(1)求函数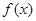 的解析式,并写出
的解析式,并写出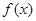 的单调减区间;
的单调减区间;
(2)记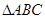 的内角
的内角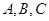 的对边长分别为
的对边长分别为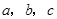 ,
,
若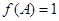 ,
,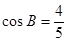 ,
,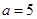 求
求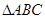 的面积.
的面积.
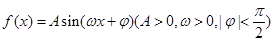 的部分图象如图所示.
的部分图象如图所示.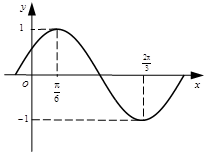
(1)求函数
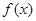 的解析式,并写出
的解析式,并写出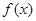 的单调减区间;
的单调减区间;(2)记
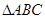 的内角
的内角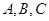 的对边长分别为
的对边长分别为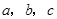 ,
,若
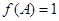 ,
,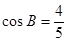 ,
,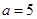 求
求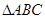 的面积.
的面积.(1) 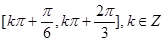 (2)
(2) 
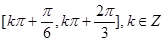 (2)
(2) 
(1)由图像可观察出A=1,然后可求出周期,进而求出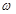 ,再根据过点
,再根据过点
 求出
求出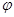 ,从而确定出f(x)的解析式,再利用正弦函数的单调增区间确定其增区间即可.
,从而确定出f(x)的解析式,再利用正弦函数的单调增区间确定其增区间即可.
(2)在(1)的基础上,根据f(A)=1,可求出A,这样就知道两角一边,可用正弦定理,求出b,再利用sinC=sin(A+B)求出sinC,最后用面积公式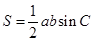 求面积即可.
求面积即可.
解:(1)由图象最高点得A=1,
由周期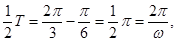
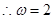 -----------2’
-----------2’
当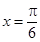 时,
时,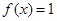 ,可得
,可得 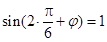 ,
,
因为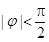 ,所以
,所以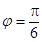 .
. 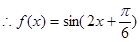 ----------4’
----------4’
由图象可得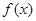 的单调减区间为
的单调减区间为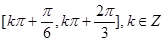 ----------6’
----------6’
(2)由(I)可知,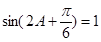 ,
,
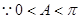 ,
, 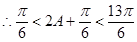 ,
, 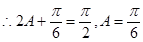 .
.
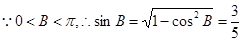 ----------9’
----------9’
由正弦定理得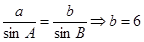 ----------10’
----------10’
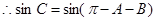
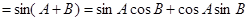
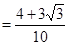
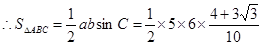
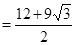 .....................12’
.....................12’
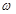 ,再根据过点
,再根据过点 求出
求出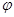 ,从而确定出f(x)的解析式,再利用正弦函数的单调增区间确定其增区间即可.
,从而确定出f(x)的解析式,再利用正弦函数的单调增区间确定其增区间即可.(2)在(1)的基础上,根据f(A)=1,可求出A,这样就知道两角一边,可用正弦定理,求出b,再利用sinC=sin(A+B)求出sinC,最后用面积公式
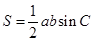 求面积即可.
求面积即可.解:(1)由图象最高点得A=1,
由周期
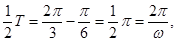
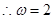 -----------2’
-----------2’当
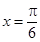 时,
时,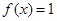 ,可得
,可得 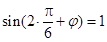 ,
,因为
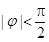 ,所以
,所以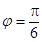 .
. 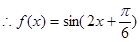 ----------4’
----------4’由图象可得
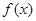 的单调减区间为
的单调减区间为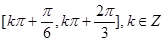 ----------6’
----------6’(2)由(I)可知,
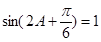 ,
, 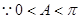 ,
, 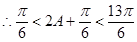 ,
, 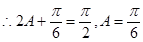 .
. 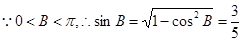 ----------9’
----------9’由正弦定理得
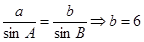 ----------10’
----------10’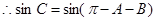
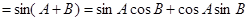
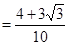
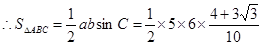
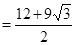 .....................12’
.....................12’
练习册系列答案
相关题目
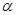 为第二象限角,则
为第二象限角,则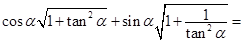 ____________
____________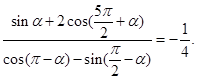
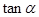 的值;
的值;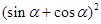 的值.
的值.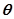 是第一象限角,试确定
是第一象限角,试确定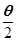 的象限.
的象限.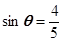 ,求
,求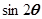 的值.
的值. 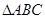 中,内角
中,内角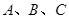 的对边的边长为
的对边的边长为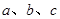 ,且
,且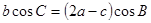 ,则
,则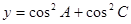 的最小值为
的最小值为 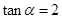 ,则
,则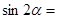 。
。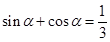 ,则
,则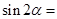 ( )
( ) 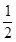
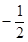

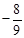
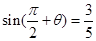 ,则
,则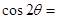 .
.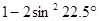 的结果等于(
的结果等于(