题目内容
已知A={(x,y)|x+y≤1,x≥0,y≥0},B={(x+y,x-2y)|(x,y)∈A},点(u,v)∈B,则2u-v的最大值为
- A.1
- B.2
- C.3
- D.4
D
分析:先画出集合A={(x,y)|x+y≤1,x≥0,y≥0}对应的平面区域,再把所求2u-v的最大值问题转化为求x+4y的最大值,结合图象即可得出结论.
解答:由题得:2u-v=2(x+y)-(x-2y)=x+4y.
画出集合A={(x,y)|x+y≤1,x≥0,y≥0}对应的平面区域如图: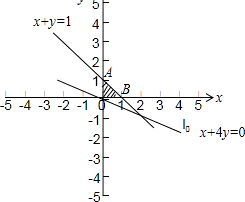
即为求z=x+4y的最大值问题.
由图得当过点A(0,1)时,x+4y有最大值是:0+4×1=4.
故选D.
点评:本题主要考查线性规划的应用.解决问题的关键在于把所求2u-v的最大值问题转化为求x+4y的最大值.
分析:先画出集合A={(x,y)|x+y≤1,x≥0,y≥0}对应的平面区域,再把所求2u-v的最大值问题转化为求x+4y的最大值,结合图象即可得出结论.
解答:由题得:2u-v=2(x+y)-(x-2y)=x+4y.
画出集合A={(x,y)|x+y≤1,x≥0,y≥0}对应的平面区域如图:
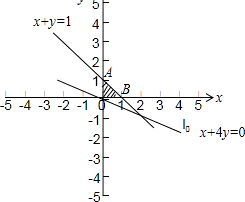
即为求z=x+4y的最大值问题.
由图得当过点A(0,1)时,x+4y有最大值是:0+4×1=4.
故选D.
点评:本题主要考查线性规划的应用.解决问题的关键在于把所求2u-v的最大值问题转化为求x+4y的最大值.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目