题目内容
已知数列{an}满足an+1=-an2+2an(n∈N*),且0<a1<1.
(1)用数学归纳法证明:0<an<1;
(2)若bn=lg(1-an),且 ,求无穷数列
,求无穷数列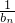 所有项的和.
所有项的和.
(1)证明:①当n=1时,由条件知,成立
②假设n=k成立,即0<ak<1成立,
当n=k+1时,ak+1=-ak2+2ak=-(ak-1)2+1,
∵0<aK<1
∴0<(ak-1)2<1
∴0<-(ak-1)2+1<1
∴0<aK+1<1
这就是说,当=k+1时,0<ak<1也成立.
根据①②知,对任意n∈N*,不等式0<an<1恒成立.
(2)解:1-an+1=(1-an)2,0<an<1;
lg(1-an+1)=lg(1-an)2,,即lg(1-an+1)=2lg(1-an)
即:bn+1=2bn
∴{bn}是以-1为首项,以2为公比的等比数列.
∴bn=-2n-1,∴
无究数列{ }所有项的和为:
}所有项的和为:
 =
= (
( )=
)= [(-1)×
[(-1)× ]=-2×
]=-2× (
( )=-2
)=-2
分析:(1)要求用数学归纳法证明:按照两个步骤进行,特别注意递推即可.
(2)由an+1=-an2+2an和bn=lg(1-an)及 ,求得bn列进而求得
,求得bn列进而求得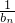 ,再取极限即可.
,再取极限即可.
点评:本题主要考查数学归纳法和等比数列的求法及无穷数学所有项的和的求法.
②假设n=k成立,即0<ak<1成立,
当n=k+1时,ak+1=-ak2+2ak=-(ak-1)2+1,
∵0<aK<1
∴0<(ak-1)2<1
∴0<-(ak-1)2+1<1
∴0<aK+1<1
这就是说,当=k+1时,0<ak<1也成立.
根据①②知,对任意n∈N*,不等式0<an<1恒成立.
(2)解:1-an+1=(1-an)2,0<an<1;
lg(1-an+1)=lg(1-an)2,,即lg(1-an+1)=2lg(1-an)
即:bn+1=2bn
∴{bn}是以-1为首项,以2为公比的等比数列.
∴bn=-2n-1,∴

无究数列{
 }所有项的和为:
}所有项的和为: =
= (
( )=
)= [(-1)×
[(-1)× ]=-2×
]=-2× (
( )=-2
)=-2分析:(1)要求用数学归纳法证明:按照两个步骤进行,特别注意递推即可.
(2)由an+1=-an2+2an和bn=lg(1-an)及
 ,求得bn列进而求得
,求得bn列进而求得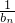 ,再取极限即可.
,再取极限即可.点评:本题主要考查数学归纳法和等比数列的求法及无穷数学所有项的和的求法.

练习册系列答案
相关题目