题目内容
a,b∈R,若关于x的方程x2+(a+bi)x+4+3i=0有实数根,则|a|的最小值是
4
4
.分析:设方程的实根为m,代入方程x2+(a+bi)x+4+3i=0,得出关于a,b的制约关系式,看作关于b的函数,求函数最值可以得出结果.
解答:解:设方程的实根为m,代入方程x2+(a+bi)x+4+3i=0得m2+(a+bi)m+4+3i=0,整理,得m2+am+4+(bm+3)i=0
所以
,易知m≠0由②得m=-
,代入①消去m
-
+4=0,∴a=
所以|a|=
≥
═
=4,当且仅当9=4b2=,b=±
时取到最小值.
故答案为:4
所以
|
| 3 |
| b |
| 9 |
| b2 |
| 3a |
| b |
| 9+4b2 |
| 3b |
所以|a|=
| 9+4b2 |
| 3|b| |
2
| ||
| 3|b| |
| 2×6|b| |
| 3|b| |
| 3 |
| 2 |
故答案为:4
点评:本题借助于复系数二次方程的根的性质,求参数范围,考查消元法,基本不等式的应用,转化能力.

练习册系列答案
相关题目
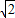 -1
-1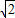 -1
-1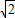 +1
+1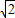 +1
+1 -1
-1 -1
-1 +1
+1 +1
+1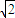 -1
-1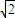 -1
-1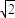 +1
+1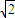 +1
+1