题目内容
 某电脑生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按40个工作时计算)生产联想、方正、海尔三种电脑共120台,且海尔至少生产20台.已知生产这些电脑产品每台所需工时和每台产值如下表:
某电脑生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按40个工作时计算)生产联想、方正、海尔三种电脑共120台,且海尔至少生产20台.已知生产这些电脑产品每台所需工时和每台产值如下表:| 电脑名称 | 联想 | 方正 | 海尔 | ||||||
| 工时 |
|
|
| ||||||
| 产值(千元) | 4 | 3 | 2 |
(Ⅱ)每周生产联想、方正、海尔各多少台,才能使产值最高,最高产值是多少?
分析:(Ⅰ)根据条件建立约束条件,并作出可行域.(Ⅱ)利用目标函数求出最优解.
解答: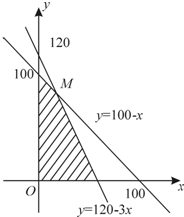 解:(Ⅰ)由题意得:生产海尔120-x-y台…(1分)
解:(Ⅰ)由题意得:生产海尔120-x-y台…(1分)
即
…(5分)
相应的平面区域如图所示…(8分)
(Ⅱ)产值z=4x+3y+2(120-x-y)=2x+y+240(9分)
由可行域知
解
得点M(10,90)…(11分)
所以生产联想10台,方正90台,海尔20台时,产值最高
最高产值为z=2×10+90+240=350(12分)
 解:(Ⅰ)由题意得:生产海尔120-x-y台…(1分)
解:(Ⅰ)由题意得:生产海尔120-x-y台…(1分)
|
|
相应的平面区域如图所示…(8分)
(Ⅱ)产值z=4x+3y+2(120-x-y)=2x+y+240(9分)
由可行域知
解
|
所以生产联想10台,方正90台,海尔20台时,产值最高
最高产值为z=2×10+90+240=350(12分)
点评:本题主要考查了简单的线性规划,以及利用几何意义求最值.

练习册系列答案
相关题目
例1某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台,已知生产家电产品每台所需工时和每台产值如下表:
问:每周应用生产空调器、彩电、冰箱各多少台,才使产值最高?最高产值多少?(以千元为单位)
| 家电名称 | 空调机 | 彩电 | 冰箱 | ||||||
| 工时 |
|
|
| ||||||
| 产值/千元 | 4 | 3 | 2 |
某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台,已知生产家电产品每台所需工时和每台产值如下表:
家电名称 | 空调器 | 彩电 | 冰箱 |
工时 |
|
|
|
产值(千元) | 4 | 3 | 2 |
问:每周应生产空调器、彩电、冰箱各多少台,才使产值最高?最高产值为多少?(以千元为单位)
某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台. 已知生产家电产品每台所需工时和每台产值如下表:
| 家电名称 | 空调器 | 彩电 | 冰箱 |
| 工时 |
|
|
|
| 产值(千元) | 4 | 3 | 2 |
问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位)
某电脑生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按40个工作时计算)生产联想、方正、海尔三种电脑共120台,且海尔至少生产20台.已知生产这些电脑产品每台所需工时和每台产值如下表:
(Ⅰ)若生产联想与方正分别是x台、y台,试写出x、y满足的条件,并在给出的直角坐标系中画出相应的平面区域.
(Ⅱ)每周生产联想、方正、海尔各多少台,才能使产值最高,最高产值是多少?
| 电脑名称 | 联想 | 方正 | 海尔 |
| 工时 |  |  |  |
| 产值(千元) | 4 | 3 | 2 |
(Ⅱ)每周生产联想、方正、海尔各多少台,才能使产值最高,最高产值是多少?
