题目内容
设M,N是球心O的半径OP上的两点,且NP=MN=OM,分别过N,M,O作垂线于OP的面截球得三个圆,则这三个圆的面积之比为:( )A.3,5,6
B.3,6,8
C.5,7,9
D.5,8,9
【答案】分析:先求截面圆的半径,然后求出三个圆的面积的比.
解答:解:设分别过N,M,O作垂线于OP的面截球得三个圆的半径为r1,r2,r3,球半径为R,则: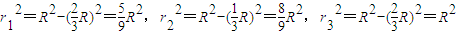
∴r12:r22:r32=5:8:9∴这三个圆的面积之比为:5,8,9
故选D
点评:此题重点考查球中截面圆半径,球半径之间的关系;考查空间想象能力,利用勾股定理的计算能力.
解答:解:设分别过N,M,O作垂线于OP的面截球得三个圆的半径为r1,r2,r3,球半径为R,则:
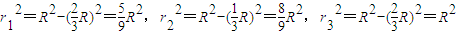
∴r12:r22:r32=5:8:9∴这三个圆的面积之比为:5,8,9
故选D
点评:此题重点考查球中截面圆半径,球半径之间的关系;考查空间想象能力,利用勾股定理的计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设M,N是球心O的半径OP上的两点,且NP=MN=OM,分别过N,M,O作垂线于OP的面截球得三个圆,则这三个圆的面积之比为:( )
| A、3,5,6 | B、3,6,8 | C、5,7,9 | D、5,8,9 |