题目内容
知集合A={x|x2-3x-10≤0},B={x|m+1≤x≤2m-1},且B≠∅.(1)若“命题p:?x∈B,x∈A”是真命题,求m的取值范围.
(2)“命题q:?x∈A,x∈B”是真命题,求m的取值范围.
【答案】分析:(1)化简集合A={x|-2≤x≤5},根据B={x|m+1≤x≤2m-1},B≠∅,p真,建立不等式组,即可求得m的取值范围;
(2)q为真,则A∩B≠∅,由于B≠∅,从而m≥2,进而可建立不等式组,即可求得m的取值范围.
解答:解:(1)A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},B≠∅
∵“命题p:?x∈B,x∈A”是真命题
∴B⊆A,B≠∅
∴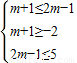 ,解得2≤m≤3
,解得2≤m≤3
(2)q为真,则A∩B≠∅,
∵B≠∅,∴m≥2
∴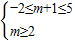
∴2≤m≤4
点评:本题考查命题真假的运用,考查学生分析解决问题的能力,考查解不等式,属于中档题.
(2)q为真,则A∩B≠∅,由于B≠∅,从而m≥2,进而可建立不等式组,即可求得m的取值范围.
解答:解:(1)A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},B≠∅
∵“命题p:?x∈B,x∈A”是真命题
∴B⊆A,B≠∅
∴
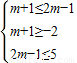 ,解得2≤m≤3
,解得2≤m≤3(2)q为真,则A∩B≠∅,
∵B≠∅,∴m≥2
∴
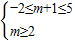
∴2≤m≤4
点评:本题考查命题真假的运用,考查学生分析解决问题的能力,考查解不等式,属于中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目