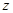题目内容
随着经济的发展,人们生活水平的提高,中学生的营养与健康问题越来越得到学校与家长的重视. 从学生体检评价报告单了解到某校3000名学生的体重发育评价情况,得右表:
|
|
偏瘦 |
正常 |
肥胖 |
|
女生(人) |
300 |
865 |
|
|
男生(人) |
|
885 |
|
已知从这批学生中随机抽取1名学生,抽到偏瘦男生的概率为0.15.
(Ⅰ)求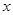 的值;
的值;
(Ⅱ)若用分层抽样的方法,从这批学生中随机抽取60名,问应在肥胖学生中抽出多少名?
(Ⅲ)已知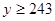 ,
,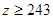 ,求肥胖学生中男生不少于女生的概率.
,求肥胖学生中男生不少于女生的概率.
【答案】
(Ⅰ) =450;(Ⅱ)应在肥胖学生中抽10名;(Ⅲ)
=450;(Ⅱ)应在肥胖学生中抽10名;(Ⅲ) .
.
【解析】
试题分析:(Ⅰ)利用“从3000名学生中随机抽取1名学生,抽到偏瘦男生的概率为0.15”可求得 ;(Ⅱ)根据分层抽样可求;(Ⅲ)利用古典概型求解.
;(Ⅱ)根据分层抽样可求;(Ⅲ)利用古典概型求解.
试题解析:(Ⅰ)由题意可知 , ∴
, ∴ =450(人)
3分
=450(人)
3分
(Ⅱ)由题意知,肥胖学生人数为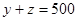 (人)。
设应在肥胖学生中抽取
(人)。
设应在肥胖学生中抽取 人,
人,
则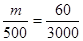 , ∴
, ∴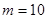 (人) 答:应在肥胖学生中抽10名 6分
(人) 答:应在肥胖学生中抽10名 6分
(Ⅲ)由题意可知, 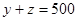 ,且
,且 ,
, ,满足条件的
,满足条件的
(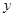 ,
, )有(243,257),(244,256),
,(257,243),共有15组。
)有(243,257),(244,256),
,(257,243),共有15组。
设事件A:“肥胖学生中男生不少于女生”,即 ,满足条件的(
,满足条件的(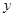 ,
, )
)
(243,257),(244,256), ,(250,250),共有8组,所以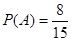 。
。
答:肥胖学生中男生不少于女生的概率为 12分
12分
考点:分层抽样,古典概率.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
随着经济的发展,人们生活水平的提高,中学生的营养与健康问题越来越得到学校与家长的重视.从学生体检评价报告单了解到我校3000名学生的体重发育评价情况,得下表:
已知从这批学生中随机抽取1名学生,抽到偏瘦男生的概率为0.15.
(1)求x的值;
(2)若用分层抽样的方法,从这批学生中随机抽取60名,问应在肥胖学生中抽多少名?
(3)已知y≥243,z≥243,肥胖学生中男生不少于女生的概率.
| 偏瘦 | 正常 | 肥胖 | |
| 女生(人) | 300 | 865 | y |
| 男生(人) | x | 885 | z |
(1)求x的值;
(2)若用分层抽样的方法,从这批学生中随机抽取60名,问应在肥胖学生中抽多少名?
(3)已知y≥243,z≥243,肥胖学生中男生不少于女生的概率.