题目内容
在锐角△ABC中，∠A，∠B，∠C所对边分别为a，b，c．已知
=（sinA，cosA），
=（cosC，sinC），且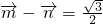
．
（1）求∠B的大小；
（2）若b=3，求a+c的最大值．
解：（1）∵
=sinAcos C+cosAsinC=sin（A+C）=sinB=
，故锐角B=
．
（2）∵B=，∴cosB=
=
，∴b2=（a+c）2-3ac=9，
∵ac≤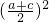
，∴9≥
，∴a+c≤6，
故a+c的最大值为 6．
分析：（1）由=sinAcos C+cosAsinC=sin（A+C）=sinB，求出sinB的值，即得锐角B 的值．
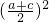（2）由cosB==，得到 （a+c）2-3ac=9，再由ac≤，可得9≥，从而得到a+c的最大值．
点评：本题考查两个向量的数量积公式，余弦定理，基本不等式的应用，得到 b2=（a+c）2-3ac=9，时间诶体的关键．
=sinAcos C+cosAsinC=sin（A+C）=sinB=，故锐角B=．（2）∵B=
，∴cosB==，∴b2=（a+c）2-3ac=9，∵ac≤
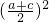，∴9≥，∴a+c≤6，故a+c的最大值为 6．
分析：（1）由
=sinAcos C+cosAsinC=sin（A+C）=sinB，求出sinB的值，即得锐角B 的值．（2）由cosB=
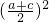=，得到 （a+c）2-3ac=9，再由ac≤，可得9≥，从而得到a+c的最大值．点评：本题考查两个向量的数量积公式，余弦定理，基本不等式的应用，得到 b2=（a+c）2-3ac=9，时间诶体的关键．
练习册系列答案
阅读快车系列答案
相关题目