题目内容
 如图,已知正方体棱长为1,求证:平面B1AD1∥平面BC1D,并写出这两个平行平面间的距离.
如图,已知正方体棱长为1,求证:平面B1AD1∥平面BC1D,并写出这两个平行平面间的距离.分析:利用面面平行的判定定理转化为证明D1B1∥平面DBC1,AD1∥平面DBC1,进而转化为证明线线平行即可;先利用线面垂直的判定定理证明A1C⊥平面B1AD1,由面面平行的性质知A1C⊥平面BC1D,设A1C分别交平面B1AD1,平面BC1D点O1,O2,则O1O2即为量平行平面间的距离,利用等积法可求得A1O1,CO2,从而可求得O1O2,即所求距离.
解答:解:因为B1B∥D1D,B1B=D1D,
所以四边形DD1B1B为平行四边形,所以D1B1∥DB,
又D1B1?面BDC1,DB?平面DBC1,
所以D1B1∥平面DBC1,
同理AD1∥平面DBC1,
又AD1∩D1B1=D1,D1B1?平面B1AD1,AD1?平面B1AD1,
所以平面B1AD1∥平面BC1D;
连接A1C,A1D,
因为CD⊥平面AA1D1D,AD1?平面AA1D1D,所以CD⊥AD1,
又AD1⊥A1D,CD∩A1D=D,
所以AD1⊥平面A1DC,
A1C?平面A1DC,所以AD1⊥A1C,
同理可证AB1⊥A1C,
又AD1∩AB1=A,所以A1C⊥平面B1AD1,
而平面B1AD1∥平面BC1D,所以A1C⊥平面BC1D,
设A1C分别交平面B1AD1,平面BC1D点O1,O2,则O1O2即为两平行平面间的距离,
在三棱锥中,VA-A1B1D1=VA1-AB1D1,即
×S△A1B1D1×AA1=
×S△AB1D1×A1O1,
所以
×1×1×1=
×(
)2×A1O1,解得A1O1=
,
根据正方体的对称性可求得CO2=
,所以O1O2=
A1C=
,
所以这两个平行平面间的距离为
.
所以四边形DD1B1B为平行四边形,所以D1B1∥DB,
又D1B1?面BDC1,DB?平面DBC1,
所以D1B1∥平面DBC1,
同理AD1∥平面DBC1,
又AD1∩D1B1=D1,D1B1?平面B1AD1,AD1?平面B1AD1,
所以平面B1AD1∥平面BC1D;
连接A1C,A1D,
因为CD⊥平面AA1D1D,AD1?平面AA1D1D,所以CD⊥AD1,
又AD1⊥A1D,CD∩A1D=D,
所以AD1⊥平面A1DC,
A1C?平面A1DC,所以AD1⊥A1C,
同理可证AB1⊥A1C,
又AD1∩AB1=A,所以A1C⊥平面B1AD1,
而平面B1AD1∥平面BC1D,所以A1C⊥平面BC1D,
设A1C分别交平面B1AD1,平面BC1D点O1,O2,则O1O2即为两平行平面间的距离,
在三棱锥中,VA-A1B1D1=VA1-AB1D1,即
| 1 |
| 3 |
| 1 |
| 3 |
所以
| 1 |
| 2 |
| ||
| 4 |
| 2 |
| ||
| 3 |
根据正方体的对称性可求得CO2=
| ||
| 3 |
| 1 |
| 3 |
| ||
| 3 |
所以这两个平行平面间的距离为
| ||
| 3 |
点评:本题考查空间点、线、面间的距离计算,考查学生的空间想象能力、计算能力及逻辑推理能力,熟记相关判定定理性质定理是解决该类题目的基础.

练习册系列答案
相关题目
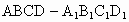 是棱长为a的正方体,E、F分别为棱
是棱长为a的正方体,E、F分别为棱 与
与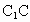 的中点,求四棱锥
的中点,求四棱锥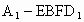 的体积.
的体积.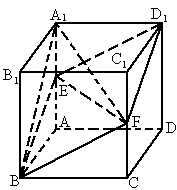
 是棱长为
是棱长为 的正方体,点
的正方体,点 在
在 上,点
上,点 在
在 上,且
上,且 .
. 四点共面;(4分)
四点共面;(4分) 在
在 上,
上,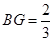 ,点
,点 在
在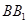 上,
上, ,垂足为
,垂足为 ,求证:
,求证: 平面
平面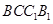 ;(4分)
;(4分) 表示截面
表示截面 和侧面
和侧面 .(4分
.(4分
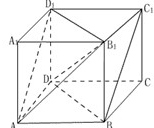 如图,已知正方体棱长为1,求证:平面B1AD1∥平面BC1D,并写出这两个平行平面间的距离.
如图,已知正方体棱长为1,求证:平面B1AD1∥平面BC1D,并写出这两个平行平面间的距离.