题目内容
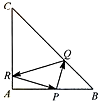 在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到点P(如图).若光线QR经过△ABC的重心(三角形三条中线的交点),则AP=
在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点,光线从点P出发,经BC,CA发射后又回到点P(如图).若光线QR经过△ABC的重心(三角形三条中线的交点),则AP=| 4 |
| 3 |
| 4 |
| 3 |
分析:建立坐标系,设点P的坐标,可得P关于直线BC的对称点P1的坐标,和P关于y轴的对称点P2的坐标,由P1,Q,R,P2四点共线可得直线的方程,由于过△ABC的重心,代入可得关于a的方程,解之可得P的坐标,进而可得AP的值.
解答: 解:建立如图所示的坐标系:
解:建立如图所示的坐标系:
可得B(4,0),C(0,4),故直线BC的方程为x+y=4,
△ABC的重心为(
,
),
设P(a,0),其中0<a<4,
则点P关于直线BC的对称点P1(x,y),满足
,
解得
,
即P1(4,4-a),易得P关于y轴的对称点P2(-a,0),
由光的反射原理可知P1,Q,R,P2四点共线,
直线QR的斜率为k=
=
,故直线QR的方程为y=
(x+a).
由于直线QR过△ABC的重心(
,
),代入化简可得3a2-4a=0,
解得a=
,或a=0(舍去),故P(
,0),故AP=
,
故答案为
.
 解:建立如图所示的坐标系:
解:建立如图所示的坐标系:可得B(4,0),C(0,4),故直线BC的方程为x+y=4,
△ABC的重心为(
| 0+0+4 |
| 3 |
| 0+4+0 |
| 3 |
设P(a,0),其中0<a<4,
则点P关于直线BC的对称点P1(x,y),满足
|
解得
|
即P1(4,4-a),易得P关于y轴的对称点P2(-a,0),
由光的反射原理可知P1,Q,R,P2四点共线,
直线QR的斜率为k=
| 4-a-0 |
| 4-(-a) |
| 4-a |
| 4+a |
| 4-a |
| 4+a |
由于直线QR过△ABC的重心(
| 4 |
| 3 |
| 4 |
| 3 |
解得a=
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
故答案为
| 4 |
| 3 |
点评:本题考查直线与点的对称问题,涉及直线方程的求解以及光的反射原理的应用,属中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目