题目内容
设不等式组 在直角坐标系中所表示的区域的面积为S,则当k>1时,
在直角坐标系中所表示的区域的面积为S,则当k>1时, 的最小值为 .
的最小值为 .
【答案】分析:先画出不等式组所表示的平面区域,然后用k表示出图形的面积,进而表示出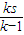 ,最后利用基本不等式求出它的最值即可.
,最后利用基本不等式求出它的最值即可.
解答: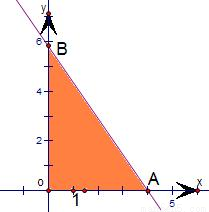 解:画出不等式组
解:画出不等式组 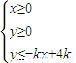 所表示的平面区域,
所表示的平面区域,
A(4,0),B(0,4k),
根据题意可知三角形OAB为直角三角形,其面积等于 ×|OA|×|OB|=8k,
×|OA|×|OB|=8k,
∴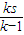 =
=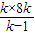 =8(
=8(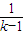 +k-1+2)≥8(2+2)=32(k>1)
+k-1+2)≥8(2+2)=32(k>1)
当且仅当k-1=1时等号,
∴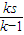 的最小值为 32,
的最小值为 32,
故答案为:32.
点评:本题考查简单的线性规划,以及利用基本不等式等知识求最值问题,是基础题.
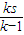 ,最后利用基本不等式求出它的最值即可.
,最后利用基本不等式求出它的最值即可.解答:
 解:画出不等式组
解:画出不等式组 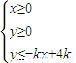 所表示的平面区域,
所表示的平面区域,A(4,0),B(0,4k),
根据题意可知三角形OAB为直角三角形,其面积等于
 ×|OA|×|OB|=8k,
×|OA|×|OB|=8k,∴
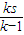 =
=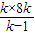 =8(
=8(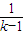 +k-1+2)≥8(2+2)=32(k>1)
+k-1+2)≥8(2+2)=32(k>1)当且仅当k-1=1时等号,
∴
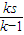 的最小值为 32,
的最小值为 32,故答案为:32.
点评:本题考查简单的线性规划,以及利用基本不等式等知识求最值问题,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在直角坐标系中所表示的区域的面积为
在直角坐标系中所表示的区域的面积为 ,则当
,则当 时,
时, 的最小值为
的最小值为  在直角坐标系中所表示的区域的面积为S,则当k>1时,
在直角坐标系中所表示的区域的面积为S,则当k>1时, 的最小值为 .
的最小值为 . 在直角坐标系中所表示的区域的面积为S,则当k>1时,
在直角坐标系中所表示的区域的面积为S,则当k>1时, 的最小值为 .
的最小值为 . 在直角坐标系中所表示的区域的面积为S,则当k>1时,
在直角坐标系中所表示的区域的面积为S,则当k>1时, 的最小值为 .
的最小值为 .