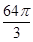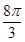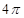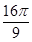题目内容
已知一个四棱锥的三视图如图所示,则该四棱锥的四个侧面中,直角三角形的个数是( )
| A.4 | B.3 | C.2 | D.1 |
A
解析试题分析:由三视图分析可知此几何体是底面为矩形且其中一条侧棱垂直与底面的四棱锥,不妨设底面为 ,侧棱
,侧棱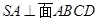 。因为
。因为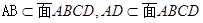 ,所以
,所以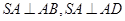 ,所以
,所以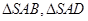 均为直角三角形。因为
均为直角三角形。因为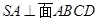 ,
,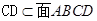 ,所以
,所以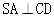 ,因为
,因为 为矩形,所以
为矩形,所以 ,因为
,因为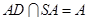 ,所以
,所以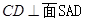 ,因为
,因为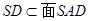 ,所以
,所以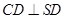 ,所以
,所以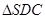 为直角三角形。同理可证
为直角三角形。同理可证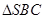 也为直角三角形。综上所得4个侧面均为直角三角形。故A正确。
也为直角三角形。综上所得4个侧面均为直角三角形。故A正确。
考点:三视图和空间几何体之间的关系,线线垂直和线面垂直。考查空间想象能力、运算求解能力

练习册系列答案
相关题目
已知几何体的三视图如图所示,它的表面积是( )
A. | B. | C. | D. |
如图是一个几何体的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的全面积为( )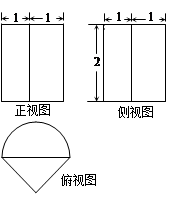
A.2+3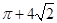 | B.2+2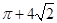 | C.8+5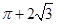 | D.6+3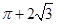 |
一个几何体的三视图如图所示,则这个几何体的体积为( )
A. | B. |
C. | D. |
设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积为 ( ).
| A.πa2 | B.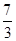 πa2 πa2 | C.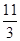 πa2 πa2 | D.5πa2 |
 的等腰直角三角形,则这个几何体的体积是( )
的等腰直角三角形,则这个几何体的体积是( )



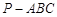 的四个顶点都在球
的四个顶点都在球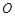 的球面上,若
的球面上,若 平面
平面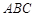 ,
,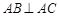 ,且
,且 ,
,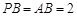 ,则球
,则球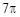
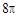
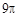
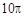
 ,过其球面上
,过其球面上 三点作截面,若
三点作截面,若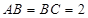 ,
,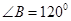 ,则球
,则球