题目内容
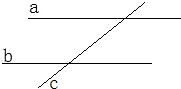
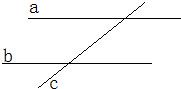
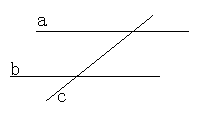
21、证明题:如图:两直线a,b平行,直线c与a,b相交,则:直线a、b、c三线共面(要求写处已知、求证、证明)
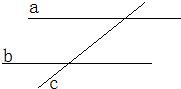

分析:这种题目首先要根据所给的图形写出符合条件的已知,求证,再根据条件进行证明,首先两条平行线确定一个平面,再说明两个交点在平面上,根据一条直线有两个点在平面上知道直线在平面上,得到三线在同一个平面上.
解答:已知:a∥b,a∩c=A,b∩c=B,
求证:直线a、b、c共面.
证明:∵a∥b
∴a与b确定一个平面α
又a∩c=A,b∩c=B,
则A∈α,B∈α
∴AB?α,即c?α,
∴直线a、b、c共面.
求证:直线a、b、c共面.
证明:∵a∥b
∴a与b确定一个平面α
又a∩c=A,b∩c=B,
则A∈α,B∈α
∴AB?α,即c?α,
∴直线a、b、c共面.
点评:本题考查平面的基本性质及推论,考查两条平行线确定一个平面,考查一条直线若有两个点在一个平面上,则直线在平面上,本题是一个基础题.

练习册系列答案
相关题目
 选做题:请考生在下列两题中任选一题作答,若两题都做,则按所做的第一题评阅计分.
选做题:请考生在下列两题中任选一题作答,若两题都做,则按所做的第一题评阅计分.