题目内容
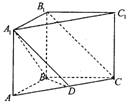
(08年大连24中) (12分) 在直三棱柱ABC―A1B1C1中,AB=BC=BB1,D为AC的中点,
(1)求证:B1C∥平面A1BD;
(2)若AC1⊥平面A1BD,二面角B―A1C1―D的余弦值.

解析:(1)连结AB1交于A1B于点E,连结ED.
∵侧面ABB1A1是正方形 ∴E是AB1的中点
又∵D是AC的中点 ∴ED∥B1C
∴B1C∥平面A1BD………………4分
(2)取A1C1的中点G,连结DG,则DG⊥A1C1
∵AB=BC ∴BD⊥AC ∴BD⊥平面A1C1D
∴BG⊥A1C1
∴∠BGD为二面角B―A1C1―D的平面角………………8分
∵AC1⊥平面A1BD,∴AC1⊥BD,又∵CC1⊥平面ABCD,且AC1在平面ABC的射影为AC,∴AC⊥BD
∵AB=BC且D为AC中点,∴AB⊥BC 且BD=![]() AB
AB
又∵DG=A1A=AB
∴BG=![]() AB ∴
AB ∴![]() ……………………12分
……………………12分

练习册系列答案
相关题目
