题目内容
已知函数 上单调递增,那么实数a的取值范围是( )
上单调递增,那么实数a的取值范围是( )A.(-∞,4)
B.(-∞,4]
C.(-∞,8)
D.(-∞,8]
【答案】分析:已知函数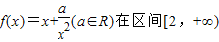 上单调递增,可得f′(x)>0在x≥2上成立,从而求出a的范围;
上单调递增,可得f′(x)>0在x≥2上成立,从而求出a的范围;
解答:解:∵函数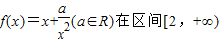 上单调递增,
上单调递增,
∴f′(x)=1-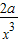 ≥0在[2,+∞)上恒成立,
≥0在[2,+∞)上恒成立,
∴a≤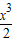 在[2,+∞)上恒成立,
在[2,+∞)上恒成立,
求出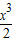 的最小值,可得其最小值为
的最小值,可得其最小值为 =4,
=4,
∴a≤4,
故选B;
点评:此题主要考查利用导数研究函数的单调性及其应用,还考查了函数的恒成立问题,解题的过程中用到了转化的思想,此题是一道中档题;
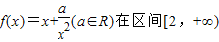 上单调递增,可得f′(x)>0在x≥2上成立,从而求出a的范围;
上单调递增,可得f′(x)>0在x≥2上成立,从而求出a的范围;解答:解:∵函数
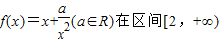 上单调递增,
上单调递增,∴f′(x)=1-
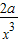 ≥0在[2,+∞)上恒成立,
≥0在[2,+∞)上恒成立,∴a≤
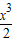 在[2,+∞)上恒成立,
在[2,+∞)上恒成立,求出
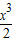 的最小值,可得其最小值为
的最小值,可得其最小值为 =4,
=4,∴a≤4,
故选B;
点评:此题主要考查利用导数研究函数的单调性及其应用,还考查了函数的恒成立问题,解题的过程中用到了转化的思想,此题是一道中档题;

练习册系列答案
相关题目

 上单调递增,在(-1,2)上单调递减,又函数
上单调递增,在(-1,2)上单调递减,又函数 .
. 的解析式;
的解析式;
 上单调递增,那么实数a的取值范围是( )
上单调递增,那么实数a的取值范围是( )